题目内容
已知圆C经过A(1,1)、B(2, )两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程.
)两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程.
(x+3)2+(y+2)2=25
解析试题分析:设圆心坐标为C(a,a+1),根据A、B两点在圆上利用两点的距离公式建立关于a的方程,解出a值,从而算出圆C的圆心和半径,可得圆C的方程.
试题解析:∵圆心在直线x-y+1=0上,
∴设圆心坐标为C(a,a+1),
根据点A(1,1)和B(2,-2)在圆上,
可得(a?1)2+(a+1?1)2=(a?2)2+(a+1+2)2,
解之得a=-3,
∴圆心坐标为C(-3,2),
半径r2=(?3?1)2+(?3+1?1)2=25,
r=5,
∴此圆的标准方程是(x+3)2+(y+2)2=25.
考点:圆的标准方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的圆心与点
的圆心与点 关于直线
关于直线 对称,直线
对称,直线 与圆
与圆 两点,且
两点,且 ,求圆
,求圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,圆
,圆 的直径为
的直径为 的长轴.如图,
的长轴.如图, 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线 过点
过点 两点,
两点, 垂直于
垂直于 .
.
 面积的最大值,并求此时直线
面积的最大值,并求此时直线 ,设点B,C是直线
,设点B,C是直线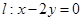 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点P在线段BC上,过P点作圆M的切线PA,切点为A
,点P在线段BC上,过P点作圆M的切线PA,切点为A  ,求直线
,求直线 的方程;
的方程; 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 (
( 为坐标原点)长的最小值
为坐标原点)长的最小值
 上的圆C.
上的圆C. 轴相切时,求圆C的方程;
轴相切时,求圆C的方程; ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围. 过点
过点 ,且圆心
,且圆心 上。
上。 : ①斜率为
: ①斜率为 ;②直线被圆
;②直线被圆 ,以
,以 过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由.
过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由. 的圆心与点
的圆心与点 关于直线
关于直线 对称,直线
对称,直线 与圆
与圆 、
、 两点,且
两点,且 ,求圆
,求圆 ,直线
,直线  ,
, 与圆
与圆 交与
交与 两点,点
两点,点 .
. 时,求
时,求 的值;
的值; 时,求
时,求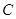 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆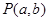 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,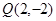 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 轴的交点为
轴的交点为 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 过点
过点