题目内容
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为,圆心在上.
的半径为,圆心在上.
(1)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标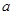 的取值范围.
的取值范围.
(1)圆C的切线方程为: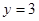 或者
或者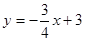 即
即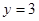 或者
或者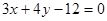 。
。
(2)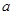 的取值范围为:
的取值范围为: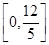 .
.
解析试题分析:
思路分析:(1)由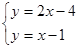 得圆心C为(3,2),设所求圆C的切线方程为
得圆心C为(3,2),设所求圆C的切线方程为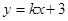 ,利用圆心到切线距离等于半径,得到k的方程,解得
,利用圆心到切线距离等于半径,得到k的方程,解得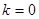 或者
或者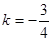 。
。
(2)首先求得圆 的方程为:
的方程为: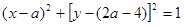 。
。
根据 得到M满足方程:
得到M满足方程: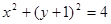 。
。
根据点M应该既在圆C上又在圆D上,即:圆C和圆D有交点。
确定a的不等式求解。
解:(1)由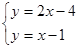 得圆心C为(3,2),
得圆心C为(3,2),
∵圆 的半径为∴圆
的半径为∴圆 的方程为:
的方程为: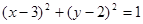 ,显然切线的斜率一定存在,设所求圆C的切线方程为
,显然切线的斜率一定存在,设所求圆C的切线方程为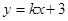 ,即
,即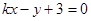 .
.
∴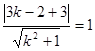 ∴
∴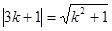 ∴
∴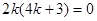 ∴
∴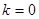 或者
或者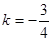 。
。
∴所求圆C的切线方程为: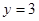 或者
或者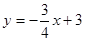 即
即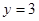 或者
或者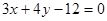 。
。
(2)解:∵圆 的圆心在在直线
的圆心在在直线 上,
上,
所以,设圆心C为(a,2a-4),则圆 的方程为:
的方程为: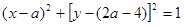 。
。
又∵ ∴设M为(x,y)则
∴设M为(x,y)则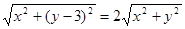 整理得:
整理得: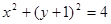 。
。
设为圆D,∴点M应该既在圆C上又在圆D上,即:圆C和圆D有交点。
∴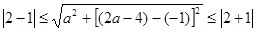 。
。
由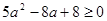 得
得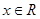 ,由
,由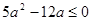 得
得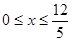 。
。
终上所述,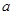 的取值范围为:
的取值范围为: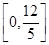 .
.
考点:直线与圆的位置关系,圆与圆的位置关系。
点评:中档题,研究直线与圆的位置关系,圆与圆的位置关系。往往利用“几何法”比较直观、简洁。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
 上的圆C.
上的圆C. 轴相切时,求圆C的方程;
轴相切时,求圆C的方程; ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围. ,直线
,直线 .
. 与圆C的位置关系;
与圆C的位置关系; ,求此时直线
,求此时直线 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 .
. 为圆心的圆与
为圆心的圆与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,其中
,其中 为坐标原点。
为坐标原点。 的面积为定值;
的面积为定值; 与圆
与圆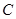 交于点
交于点 ,若
,若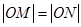 ,求圆
,求圆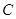 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆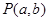 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,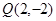 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 轴的交点为
轴的交点为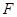 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 过点
过点 在极坐标系中的方程为
在极坐标系中的方程为 ,圆C在极坐标系中的方程为
,圆C在极坐标系中的方程为 ,求圆C被直线
,求圆C被直线 ,B(
,B( ), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标.
), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标. ,直线
,直线 以及
以及 上一点
上一点 .
.
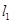 上且与直线
上且与直线 的圆⊙M的方程.
的圆⊙M的方程. 分别与直线
分别与直线 、圆⊙依次相交于A、B、C三点,
、圆⊙依次相交于A、B、C三点, .
.