题目内容
设函数f(x)=ax-(1+a2)x2,其中a>0,区间I={x|f(x)>0}.
(1)求I的长度(注:区间(α,β)的长度定义为β-α);
(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I的长度的最小值.
(1)求I的长度(注:区间(α,β)的长度定义为β-α);
(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I的长度的最小值.
(1)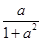 (2)
(2)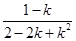
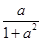 (2)
(2)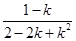
(1)令f(x)=x[a-(1+a2)x]=0,
解得x1=0,x2=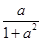 ,∴I=
,∴I=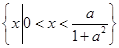 ,∴I的长度为x2-x1=
,∴I的长度为x2-x1=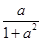 .
.
(2)k∈(0,1),则0<1-k≤a≤1+k<2.
由(1)知I的长度为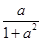 ,设g(a)=
,设g(a)=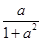 ,令g′(a)=
,令g′(a)=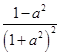 >0,则0<a<1.
>0,则0<a<1.
故g(a)关于a在[1-k,1)上单调递增,在(1,1+k]上单调递减.
g(1-k)=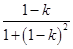 =
=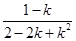 ,g(1+k)=
,g(1+k)=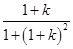 ,
,
故g(a)min=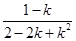 ,即I的长度的最小值为
,即I的长度的最小值为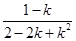
解得x1=0,x2=
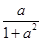 ,∴I=
,∴I=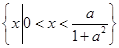 ,∴I的长度为x2-x1=
,∴I的长度为x2-x1=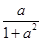 .
.(2)k∈(0,1),则0<1-k≤a≤1+k<2.
由(1)知I的长度为
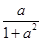 ,设g(a)=
,设g(a)=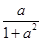 ,令g′(a)=
,令g′(a)=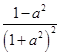 >0,则0<a<1.
>0,则0<a<1.故g(a)关于a在[1-k,1)上单调递增,在(1,1+k]上单调递减.
g(1-k)=
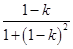 =
=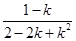 ,g(1+k)=
,g(1+k)=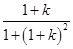 ,
,故g(a)min=
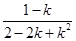 ,即I的长度的最小值为
,即I的长度的最小值为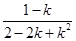

练习册系列答案
相关题目
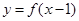 是定义在
是定义在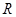 上的奇函数,则不等式
上的奇函数,则不等式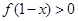 的解集为( )
的解集为( )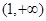
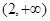
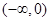
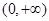
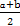 )
)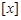 表示不超过
表示不超过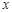 的最大整数,例如:[3.1]=3,[
的最大整数,例如:[3.1]=3,[ 2.6]=
2.6]=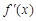 是函数
是函数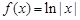 导函数,设
导函数,设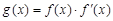 ,则函数
,则函数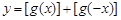 的值域是( )
的值域是( )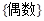
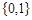
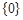
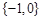
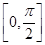 上单调递增,在区间
上单调递增,在区间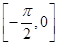 上单调递减.其中是真命题的是________.(写出所有真命题的序号)
上单调递减.其中是真命题的是________.(写出所有真命题的序号)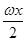 +2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
+2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
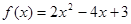 ,若
,若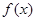 在区间[
在区间[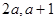 ]上不单调,则
]上不单调,则 的取值范围是
的取值范围是