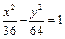��Ŀ����
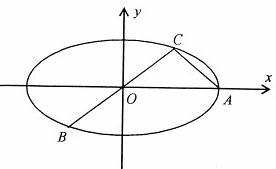
��F1��F2�ֱ�����ԲC��
+
=1��a��b��0�������ҽ��㣬
��1������ԲC�ϵĵ㣨
��
����F1��F2�������֮�͵���4��д����ԲC�ķ��̺ͽ�������
��2����K�ǣ�1����������Բ�ϵĶ��㣬���߶�KF1���е�B�Ĺ켣����
��3�����P����ԲC�ϵ�����һ�㣬��ԭ���ֱ��L����Բ�ཻ��M��N���㣬��ֱ��PM��PN��б�ʶ����ڣ�����ΪkPM��KPN��̽��kPM•KPN��ֵ�Ƿ����P��ֱ��L�йأ���֤����Ľ��ۣ�
| x2 |
| a2 |
| y2 |
| b2 |
��1������ԲC�ϵĵ㣨
| 3 |
| ||
| 2 |
��2����K�ǣ�1����������Բ�ϵĶ��㣬���߶�KF1���е�B�Ĺ켣����
��3�����P����ԲC�ϵ�����һ�㣬��ԭ���ֱ��L����Բ�ཻ��M��N���㣬��ֱ��PM��PN��б�ʶ����ڣ�����ΪkPM��KPN��̽��kPM•KPN��ֵ�Ƿ����P��ֱ��L�йأ���֤����Ľ��ۣ�
��1�����ڵ�(
��
)����Բ�ϣ�
+
=1
2a=4��
��ԲC�ķ���Ϊ
+
=1
��������ֱ�Ϊ��-1��0������1��0��
��2����KF1���е�ΪB��x��y�����K��2x+1��2y��
��K�����������Բ
+
=1�е�
+
=1
�߶�KF1���е�B�Ĺ켣����Ϊ(x+
)2+
=1
��3����ԭ���ֱ��L����Բ�ཻ������M��N��������ԭ��Գ�
��M��x0��y0��N��-x0��-y0����p��x��y��
M��N��P����Բ�ϣ�Ӧ������Բ���̣�
��
+
=1��
+
=1
kPM=
��KPN=
kPM•KPN=
•
=
=-
kPM•KPN��ֵ���P��ֱ��L��
| 3 |
| ||
| 2 |
(
| ||
| a2 |
(
| ||||
| b2 |
2a=4��
��ԲC�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��������ֱ�Ϊ��-1��0������1��0��
��2����KF1���е�ΪB��x��y�����K��2x+1��2y��
��K�����������Բ
| x2 |
| 4 |
| y2 |
| 3 |
| (2x+1)2 |
| 4 |
| (2y)2 |
| 3 |
�߶�KF1���е�B�Ĺ켣����Ϊ(x+
| 1 |
| 2 |
| y2 | ||
|
��3����ԭ���ֱ��L����Բ�ཻ������M��N��������ԭ��Գ�
��M��x0��y0��N��-x0��-y0����p��x��y��
M��N��P����Բ�ϣ�Ӧ������Բ���̣�
��
| x02 |
| a2 |
| y02 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
kPM=
| y-y0 |
| x-x0 |
| y+y0 |
| x+x0 |
kPM•KPN=
| y-y0 |
| x-x0 |
| y+y0 |
| x+x0 |
| y2-y02 |
| x2-x02 |
| b2 |
| a2 |
kPM•KPN��ֵ���P��ֱ��L��

��ϰ��ϵ�д�
 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
�����Ŀ
 ����Բ������
����Բ������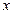 ���ϵ���Բ
���ϵ���Բ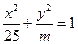 ���ӽ���Բ����
���ӽ���Բ����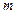 �ķ�Χ��
�ķ�Χ��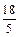 �ľ���֮����
�ľ���֮����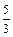 �����P�Ĺ켣�����ǣ� ��
�����P�Ĺ켣�����ǣ� ��