题目内容
1.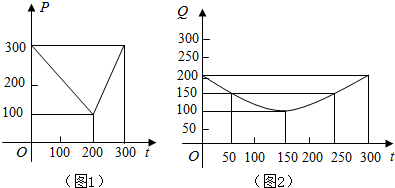 某种蔬菜基地种植西红柿由历年市场行情得知,从2月1日起的300天内,西红柿市场售价p与上市时间t的关系图是一条折线(如图(1)),种植成本Q与上市时间t的关系是一条抛物线(如图(2)).
某种蔬菜基地种植西红柿由历年市场行情得知,从2月1日起的300天内,西红柿市场售价p与上市时间t的关系图是一条折线(如图(1)),种植成本Q与上市时间t的关系是一条抛物线(如图(2)).(1)写出西红柿的市场售价与时间的函数解析式p=f(t).
(2)写出西红柿的种植成本与时间的函数解析式Q=g(t).
(3)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
分析 (1)本题是一次函数的分段函数,运用一次函数的解析式,即可得到所求;
(2)运用二次函数的解析式,解方程可得,写出自变量的范围;
(3)基本等量关系是:纯收益=市场售价-种植成本.由于P是分段函数,所以h也是分段函数,求最大利润,就要在每一个分段函数内,根据自变量取值范围,函数性质来确定.
解答 解:(1)由图-设f(t)=kt+300,(0≤t≤200),
代入(200,100),可得k=-1;
设f(t)=mt+b,200<t≤300,代入(200,100),(300,300),
可得100=200m+b,300m+b=300,解得m=2,b=-300.
可得市场售价与时间的函数关系为
P=f(t)=$\left\{\begin{array}{l}{300-t,0≤t≤200}\\{2t-300,200<t≤300}\end{array}\right.$;
(2)由图二可得可设g(t)=a(t-150)2+100,
代入点(50,150),解得a=$\frac{1}{200}$,
则种植成本与时间的函数关系为
Q=g(t)=$\frac{1}{200}$(t-150)2+100,0≤t≤300;
(3)设t时刻的纯收益为h,则由题意得h=P-Q,即
h=$\left\{\begin{array}{l}{-\frac{1}{200}{t}^{2}+\frac{1}{2}t+\frac{175}{2},0≤t≤200}\\{-\frac{1}{200}{t}^{2}+\frac{7}{2}t-\frac{1025}{2},200<t≤300}\end{array}\right.$,
当0≤t≤200时,配方整理得h=-$\frac{1}{200}$(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100
当200<t≤300时,配方整理得h=-$\frac{1}{200}$(t-350)2+100,
所以,当t=300时,h取得区间[200,300]上的最大值87.5,
综上,由100>87.5可知,h在区间[0,300]上可以取得最大值100,
此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
点评 本题考查一次函数与分段函数,二次函数,自变量取值范围在本题中都得到了体现,要根据题目给的范围,找准等量关系,分段求最大值.

| A. | [$\frac{1}{6}$,$\frac{1}{3}$] | B. | [0,$\frac{1}{3}$] | C. | [0,$\frac{1}{3}$) | D. | [$\frac{1}{6}$,$\frac{1}{3}$) |
| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}$≥2 | B. | 当x>0且x≠1时,$\sqrt{x}$+$\frac{1}{\sqrt{x}}$≥2 | ||
| C. | 当x≥3时,x+$\frac{1}{x}$的最小值是$\frac{10}{3}$ | D. | 当0<x≤1时,x-$\frac{1}{x}$无最大值 |
 如图,在长为10千米的河流OC的一侧有一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数y=ax2+bx+c(a≠0),x∈[0,6](单位:千米)的图象,且图象的最高点为A(4,4);观光带的后一部分为线段BC.
如图,在长为10千米的河流OC的一侧有一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数y=ax2+bx+c(a≠0),x∈[0,6](单位:千米)的图象,且图象的最高点为A(4,4);观光带的后一部分为线段BC.