题目内容
13．已知圆ρ=2，直线ρcosθ=4，过极点作射线交圆于点A，交直线于点B，当射线以极点为中心转动时，求线段AB的中点M的轨迹方程．分析 如图所示，设M（ρ，θ），则A（2，θ），B（2ρ-2，θ）．可得（2ρ-2）cosθ=4，即可得出．
解答 
解：如图所示，
设M（ρ，θ），则A（2，θ），B（2ρ-2，θ）．
∴（2ρ-2）cosθ=4，
化为（ρ-1）cosθ=2，
∴线段AB的中点M的轨迹方程为（ρ-1）cosθ=2．
点评 本题考查了极坐标方程的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
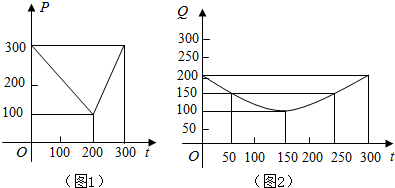某种蔬菜基地种植西红柿由历年市场行情得知，从2月1日起的300天内，西红柿市场售价p与上市时间t的关系图是一条折线（如图（1）），种植成本Q与上市时间t的关系是一条抛物线（如图（2））．
8．若对任意的实数x，都有acosx-bsinx=1，则（ ）
| A． | $\frac{1}{a^2}+\frac{1}{b^2}$≥1 | B． | $\frac{1}{a^2}+\frac{1}{b^2}$≤1 | C． | a2+b2≥1 | D． | a2+b2≤1 |