题目内容
11. 如图,在长为10千米的河流OC的一侧有一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数y=ax2+bx+c(a≠0),x∈[0,6](单位:千米)的图象,且图象的最高点为A(4,4);观光带的后一部分为线段BC.
如图,在长为10千米的河流OC的一侧有一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数y=ax2+bx+c(a≠0),x∈[0,6](单位:千米)的图象,且图象的最高点为A(4,4);观光带的后一部分为线段BC.(1)求函数为曲线段OABC的函数y=f(x),x∈[0,10]的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP,PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
分析 (1)曲线段OAB过点O,且最高点为A(4,4),可得$\left\{\begin{array}{l}c=0\\ 16a+4b+c=4\\-\frac{b}{2a}=4\end{array}\right.$,求出a,b,c,可得x∈[0,6]时的解析式;后一部分为线段BC,B(6,3),C(10,0),可得x∈[6,10]时的解析式;
(2)求出绿化带的总长度,可得二次函数,即可得出结论.
解答 解:(1)因为曲线段OAB过点O,且最高点为A(4,4),
所以$\left\{\begin{array}{l}c=0\\ 16a+4b+c=4\\-\frac{b}{2a}=4\end{array}\right.$,解得$\left\{\begin{array}{l}a=-\frac{1}{4}\\ b=2\\ c=0\end{array}\right.$
所以,当x∈[0,6]时,$y=-\frac{1}{4}{x^2}+2x$…(3分)
因为后一部分为线段BC,B(6,3),C(10,0),当x∈[6,10]时,$y=-\frac{3}{4}x+\frac{15}{2}$…(6分)
综上,$f(x)=\left\{\begin{array}{l}-\frac{1}{4}{x^2}+2x,x∈[0,6]\\-\frac{3}{4}x+\frac{15}{2},x∈(6,10]\end{array}\right.$…(8分)
(2)设OM=t(0<t≤2),则$MQ=-\frac{1}{4}{t^2}+2t,PN=-\frac{1}{4}{t^2}+2t$
由$PN=-\frac{1}{4}{t^2}+2t=-\frac{3}{4}x+\frac{15}{2}$,得$x=\frac{1}{3}{t^2}-\frac{8}{3}t+10$,
所以点$N(\frac{1}{3}{t^2}-\frac{8}{3}t+10,0)$ …(11分)
所以,绿化带的总长度y=MQ+QP+PN=$2(-\frac{1}{4}{t^2}+2t)+(\frac{1}{3}{t^2}-\frac{11}{3}t+10)=-\frac{1}{6}{t^2}+\frac{1}{3}t+10$…(13分)
当t=1时,${y_{max}}=\frac{61}{6}$
所以,当OM长为1千米时,绿化带的总长度最长 …(16分)
点评 本题考查函数解析式的确定,考查学生利益数学知识解决实际问题,属于中档题.

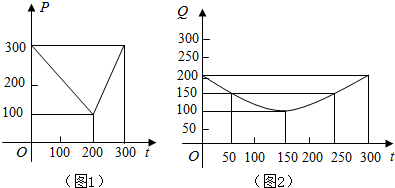 某种蔬菜基地种植西红柿由历年市场行情得知,从2月1日起的300天内,西红柿市场售价p与上市时间t的关系图是一条折线(如图(1)),种植成本Q与上市时间t的关系是一条抛物线(如图(2)).
某种蔬菜基地种植西红柿由历年市场行情得知,从2月1日起的300天内,西红柿市场售价p与上市时间t的关系图是一条折线(如图(1)),种植成本Q与上市时间t的关系是一条抛物线(如图(2)).