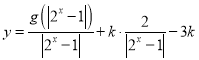题目内容
【题目】已知抛物线C：y=ax2（a＞0）的焦点到准线的距离为 
，且C上的两点A（x1 ， y1），B（x2 ， y2）关于直线y=x+m对称，并且 
，那么m= ．
【答案】
【解析】解：∵抛物线C：y=ax2（a＞0）的焦点到准线的距离为 
，
∴ 
，解得a=2．
∴抛物线C的方程为：y=2x2（a＞0）．
∵抛物线C上的两点A（x1，y1），B（x2，y2）关于直线y=x+m对称，
∴可设直线AB的方程为y=﹣x+t．
联立 
，消去y得2x2+x﹣t=0，
∵直线AB与抛物线相较于不同两点，∴△=1+4t＞0．
据根与系数的关系得， 
， 
，由已知 
，∴t=1．
于是直线AB的方程为y=﹣x+1，
设线段AB的中点为M（xM，yM），则 
= 
，
∴yM= 
= 
．
把M 
代入直线y=x+m得 
，解得m= ．
所以答案是 ．
练习册系列答案
考前必练系列答案
相关题目
