Question

【题目】用“斜二测”画法画出△ABC（A为坐标原点，AB在x轴上）的直观图为△A′B′C′，则△A′B′C′的面积与△ABC的面积的比为（ ）
A.
B.
C.
D.

Answer 1

【答案】C
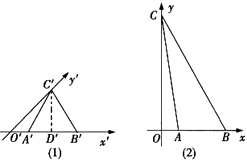
【解析】解：将△A'B'C'放入锐角为45°的斜角坐标系x'o'y'内，如图（1）所示，

过C'作C'D'⊥A'B'，垂足为D'，

将其还原为真实图形，得到图（2）的△ABC，

其中OA=O'A'，AB=A'B'，OC=2O'C'，

在△OC'D'中，O'C'= = CD，即CD= O'C'= OC，

∴△ABC的高等于OC

由此可得△ABC的面积S= ABOC，

∵直观图中△A'B'C'的面积为S= AB OC，

∴直观图和真实图形的面积的比值等于 ，

所以答案是：C．

【考点精析】利用平面图形的直观图和斜二测法画直观图对题目进行判断即可得到答案，需要熟知要画好对应平面图形的直观图，首先应在原图形中确定直角坐标系，然后在此基础上画出水平放置的平面坐标系；斜二测画法的步骤：（1）平行于坐标轴的线依然平行于坐标轴；（2）平行于y轴的线长度变半，平行于x，z轴的线长度不变；（3）画法要写好．