题目内容
4.数列{an}中,a3=2,a7=1,又数列$\left\{{\frac{1}{{{a_n}+1}}}\right\}$是等差数列,则a8=( )| A. | $\frac{11}{13}$ | B. | 0 | C. | $\frac{2}{3}$ | D. | -1 |
分析 根据数列$\left\{{\frac{1}{{{a_n}+1}}}\right\}$是等差数列,求出数列$\left\{{\frac{1}{{{a_n}+1}}}\right\}$的公差,进行求解即可.
解答 解:∵数列$\left\{{\frac{1}{{{a_n}+1}}}\right\}$是等差数列,
∴数列的第三项为$\frac{1}{{a}_{3}+1}$=$\frac{1}{2+1}$=$\frac{1}{3}$,第七项为$\frac{1}{{a}_{7}+1}=\frac{1}{1+1}$=$\frac{1}{2}$,
则设公差为d,则$\frac{1}{2}$=$\frac{1}{3}$+4d,
即4d=$\frac{1}{2}-\frac{1}{3}$=$\frac{1}{6}$,则d=$\frac{1}{24}$,
则$\frac{1}{{a}_{8}+1}$=$\frac{1}{2}+d=\frac{1}{2}+$$\frac{1}{24}$=$\frac{13}{24}$,
则a8+1=$\frac{24}{13}$,
即a8=$\frac{24}{13}$-1=$\frac{11}{13}$,
故选:A.
点评 本题主要考查等差数列的应用,根据条件结合等差数列的通项公式求出公差是解决本题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
14.观察两个变量(存在线性相关关系)得如下数据:
则两变量间的线性回归方程为( )
| x | -10 | -6.99 | -5.01 | -2.98 | 3.98 | 5 | 7.99 | 8.01 |
| y | -9 | -7 | -5 | -3 | 4.01 | 4.99 | 7 | 8 |
| A. | $\hat y$=$\frac{1}{2}$x+1 | B. | $\hat y$=x | C. | $\hat y$=2x+$\frac{1}{3}$ | D. | $\hat y$=x+1 |
15.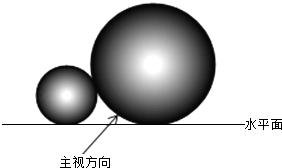 如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
 如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )| A. | 10cm | B. | 24cm | C. | 26cm | D. | 52cm |
19.若(2x-1)2013=a0+a1x+a2x2+…+a2013x2013(x∈R),则$\frac{1}{2}$+$\frac{{a}_{2}}{{2}^{2}{a}_{1}}$+$\frac{{a}_{3}}{{2}^{3}{a}_{1}}$+…+$\frac{{a}_{2013}}{{2}^{2013}{a}_{1}}$=( )
| A. | -$\frac{1}{2013}$ | B. | $\frac{1}{2013}$ | C. | -$\frac{1}{4026}$ | D. | $\frac{1}{4026}$ |
9.已知2α是第二象限角,那么α是( )
| A. | 第一象限角 | B. | 第一象限角或第三象限角 | ||
| C. | 第三象限角 | D. | 第二象限角或第四象限角 |
16.已知等差数列{an},首项a1>0,a2011+a2012>0,a2011•a2012<0,则使数列{an}的前n项和Sn>0成立的最大正整数n是( )
| A. | 2011 | B. | 2012 | C. | 4023 | D. | 4022 |