题目内容
15.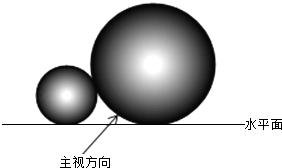 如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )| A. | 10cm | B. | 24cm | C. | 26cm | D. | 52cm |
分析 根据两球相切,可得球心距,根据两圆相切,可得圆心距是半径的和,根据根据勾股定理,可得答案.
解答 解:球心距是(36+16)÷2=26cm,
两球半径之差是(36-16)÷2=10cm,
俯视图的圆心距是$\sqrt{2{6}^{2}-1{0}^{2}}$=24cm,
故选:B.
点评 本题考查了简单组合体的三视图,利用勾股定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.要得到y=tan(2x-$\frac{π}{3}$)的图象,只要将y=tan2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
4.数列{an}中,a3=2,a7=1,又数列$\left\{{\frac{1}{{{a_n}+1}}}\right\}$是等差数列,则a8=( )
| A. | $\frac{11}{13}$ | B. | 0 | C. | $\frac{2}{3}$ | D. | -1 |
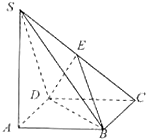 如图,四棱锥S-ABCD的底面是正方形,SA⊥平面ABCD,SA=$\sqrt{2}$AB,点E在棱SC上.
如图,四棱锥S-ABCD的底面是正方形,SA⊥平面ABCD,SA=$\sqrt{2}$AB,点E在棱SC上.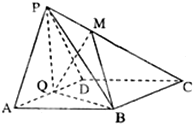 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,且Q为AD的中点.PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,且Q为AD的中点.PA=PD=AD=2.