题目内容
17.已知sinx+siny=$\frac{1}{3}$,则siny-cos2x的最小值为-$\frac{11}{12}$.分析 由条件利用同角三角函数的基本关系,正弦函数的值域、二次函数的性质,求得要求式子的最小值.
解答 解:∵sinx+siny=$\frac{1}{3}$,则siny-cos2x=$\frac{1}{3}$-sinx-cos2x=sin2x-sinx-$\frac{2}{3}$=${(sinx-\frac{1}{2})}^{2}$-$\frac{11}{12}$,
∴当sinx=$\frac{1}{2}$时,siny-cos2x取得最小值为-$\frac{11}{12}$,
故答案为:-$\frac{11}{12}$.
点评 本题主要考查同角三角函数的基本关系,正弦函数的值域、二次函数的性质,属于基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
8.记者要为5名志愿者和2名老人拍照,要求排成一排,2位老人相邻但不排在两端的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{4}{21}$ | C. | $\frac{1}{7}$ | D. | $\frac{2}{21}$ |
19.某学校在高一、高二两个年级学生中各抽取100人的样本,进行普法知识调查,其结果如下表:
(1)求x、y的值;
(2)有没有99%的把握认为“高一、高二两个年级这次普法知识调查结果有差异”;(3)用分层抽样的方法从样本的不合格同学中抽取5人的辅导小组,在5人中随机选2人,这2人中正好高一、高二各1人的概率为多少.
参考公式:${Χ^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 高一 | 高二 | 总数 | |
| 合格人数 | 70 | x | 150 |
| 不合格人数 | y | 20 | 50 |
| 总数 | 100 | 100 | 200 |
(2)有没有99%的把握认为“高一、高二两个年级这次普法知识调查结果有差异”;(3)用分层抽样的方法从样本的不合格同学中抽取5人的辅导小组,在5人中随机选2人,这2人中正好高一、高二各1人的概率为多少.
参考公式:${Χ^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| Χ2≥ | 5.024 | 6.635 | 7.879 | 10.828 |
| 97.5% | 99% | 99.5% | 99.9% |
20.若关于x的不等式ex-ax-b≥0对任意实数x恒成立,则ab的最大值为( )
| A. | $\sqrt{e}$ | B. | e2 | C. | e | D. | $\frac{e}{2}$ |
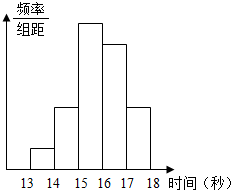 某年级200名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果以1为组距分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积依次为0.05,0.15,0.35,x,0.15,那么x=0.30;早这次百米测试中,成绩大于等于17秒的学生人数为30.
某年级200名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果以1为组距分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积依次为0.05,0.15,0.35,x,0.15,那么x=0.30;早这次百米测试中,成绩大于等于17秒的学生人数为30.