题目内容
19.某学校在高一、高二两个年级学生中各抽取100人的样本,进行普法知识调查,其结果如下表:| 高一 | 高二 | 总数 | |
| 合格人数 | 70 | x | 150 |
| 不合格人数 | y | 20 | 50 |
| 总数 | 100 | 100 | 200 |
(2)有没有99%的把握认为“高一、高二两个年级这次普法知识调查结果有差异”;(3)用分层抽样的方法从样本的不合格同学中抽取5人的辅导小组,在5人中随机选2人,这2人中正好高一、高二各1人的概率为多少.
参考公式:${Χ^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| Χ2≥ | 5.024 | 6.635 | 7.879 | 10.828 |
| 97.5% | 99% | 99.5% | 99.9% |
分析 (1)利用表格,即可求x、y的值;
(2)计算Χ2≈2.67<6.635,即可得出没有99%的把握认为“高一、高二两个年级这次普法知识调查结果有差异”;
(3)用分层抽样的方法,高一3人,设为A、B、C,高二2人,设为1、2,即可求出这2人中正好高一、高二各1人的概率为多少.
解答 解:(1)x=150-70=80,y=50-20=30.…(4分)
(2)Χ2=$\frac{200×(70×20-80×30)^{2}}{100×100×150×50}$≈2.67<6.635,
∴没有99%的把握认为“高一、高二两个年级这次普法知识调查结果有差异”;…(8分)
(3)高一3人,设为A、B、C,高二2人,设为1、2.
则符合情况的选法有:(AB)(AC)(A1)(A2)(BC)(B1)(B2)(C1)(C2)(12).
∴这2人中正好高一、高二各1人的概率为$P=\frac{3}{5}$.…(12分)
点评 本题考查概率知识的运用,考查独立性检验的应用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2012}$的值的一个程序框图,则判断框内应填入的条件是( ) 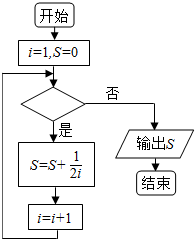

| A. | i≤1 005? | B. | i>1 005? | C. | i≤1 006? | D. | i>1 006? |
14.一个几何体的三视图如图所示,其表面积为( )
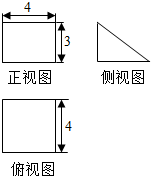

| A. | 24 | B. | 72 | C. | 60 | D. | 48 |
8.已知幂函数过点(2,$\sqrt{2}$),则当x=8时的函数值是( )
| A. | 2$\sqrt{2}$ | B. | $±2\sqrt{2}$ | C. | 2 | D. | 64 |