题目内容
12.若过点P1(2,3),P2(6,-1)的直线上一点P使|$\overrightarrow{P{P}_{1}}$|:|$\overrightarrow{P{P}_{2}}$|=3,求点P的坐标.分析 本题考查的知识点是线段的定比分点,处理的方法是:分类讨论,分P为内分点和P为内分点两种情况,计算出对应的λ值,然后代入定比分点公式进行求解.
解答 解:①若P点在线段P1P2上,则λ=3
此时$\left\{\begin{array}{l}{x=\frac{2+3×6}{1+3}=5}\\{y=\frac{3-3}{1+3}=0}\end{array}\right.$,此时P点坐标为:(5,0)
②若P点在线段P1P2的延长线上,则λ=-3
此时$\left\{\begin{array}{l}{x=\frac{2-18}{1-3}=8}\\{y=\frac{3+3}{1-3}=-3}\end{array}\right.$,
此时P点坐标为:(8,-3)
综上所述,满足条件的P点坐标为:(5,0)或(8,-3).
点评 如果已知,有向线段A(x1,y1),B(x2,y2).及点C分线段AB所成的比,求分点C的坐标,可将A,B两点的坐标代入定比分点坐标公式进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.一个几何体的三视图如图所示,其表面积为( )
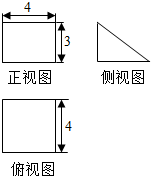

| A. | 24 | B. | 72 | C. | 60 | D. | 48 |
15.若方程x2+y2-2x-4y+m=0表示圆,则m的取值范围是( )
| A. | m≥5 | B. | m≤5 | C. | m>5 | D. | m<5 |