题目内容
2.比较大小:sin$\frac{3π}{5}$>cos$\frac{π}{5}$.分析 利用诱导公式,将两个三角函数式均化为锐角的余弦,结合余弦函数的单调性,可得答案.
解答 解:sin$\frac{3π}{5}$=sin(π-$\frac{3π}{5}$)=sin$\frac{2π}{5}$=cos($\frac{π}{2}$-$\frac{2π}{5}$)=cos$\frac{π}{10}$,
函数y=cosx在[0,$\frac{π}{2}$]上为减函数,
故cos$\frac{π}{10}$>cos$\frac{π}{5}$,
即sin$\frac{3π}{5}$>cos$\frac{π}{5}$.
故答案为:>.
点评 本题考查的知识点是诱导公式,余弦函数的图象和性质,难度中档.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
12.函数y=cos($\frac{π}{2}$-x),x∈[-π,$\frac{π}{2}$]的单调性是( )
| A. | 在[-π,-$\frac{π}{2}$]上是减函数,在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数 | |
| B. | 在[-π,0]上是减函数,在[0,$\frac{π}{2}$]上是增函数 | |
| C. | 在[-π,-$\frac{π}{2}$]上是增函数,在[-$\frac{π}{2}$,$\frac{π}{2}$]上是减函数 | |
| D. | 在[-π,0]上是增函数,在[0,$\frac{π}{2}$]上是减函数 |
7.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2012}$的值的一个程序框图,则判断框内应填入的条件是( ) 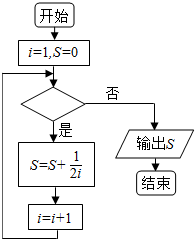

| A. | i≤1 005? | B. | i>1 005? | C. | i≤1 006? | D. | i>1 006? |