Question

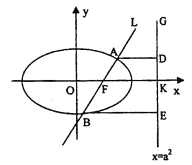
【题目】如图，已知直线的右焦点，且交椭圆于两点，点在直线上的射影依次为点.

（Ⅰ）已知抛物线的焦点为椭圆的上顶点。

①求椭圆的方程；

②若直线交轴于点，且，当变化时，求的值；

（Ⅱ）连接，试探索当变化时，直线是否相交于一定点？若交于定点，请求出点的坐标并给予证明；否则说明理由.

Answer 1

【答案】（Ⅰ）；（Ⅱ）定点.

【解析】

（1）①先由已知得以及，即可求出椭圆的方程；

②由直线交轴于点，设，由，知，然后由根与系数的关系能求出的值；
（2）当，求出点的坐标，再猜想：当变化时，相交于此定点．先利用斜率相等证明三点共线同理可得 三点共线，即可证明结论．

（Ⅰ）易知，

,设

又由

，同理

（Ⅱ）,先探索，当m=0时，直线l⊥ox轴，则ABED为矩形，由对称性知，AE与BD相交FK中点N，且

猜想：当m变化时，AE与BD相交于定点

证明：设，当m变化时首先AE过定点N

A、N、E三点共线，

同理可得B、N、D三点共线

∴AE与BD相交于定点