题目内容
【题目】如图，一个圆锥的底面半径为1，高为3，在圆锥中有一个半径为x的内接圆柱.
(1)试用x表示圆柱的高；
(2)当x为何值时，圆柱的侧面积最大，最大侧面积是多少？
【答案】（1）h＝3－3x（2）当
时，它的侧面积最大为
π
【解析】
(1)利用圆锥轴截面的特征可得圆柱的高h可表示为h＝3－3x.
(2)由题意可得S圆柱侧＝6π(x－x2)，利用二次函数的性质可得当圆柱的底面半径为时，它的侧面积最大为π.
(1)设所求的圆柱的底面半径为x，它的轴截面如图，
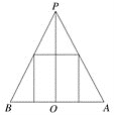
BO＝1，PO＝3，圆柱的高为h，
由图，得
＝
，即h＝3－3x.
(2)∵S圆柱侧＝2πhx＝2π(3－3x)x＝6π(x－x2)，
当x＝时，圆柱的侧面积取得最大值为π.
∴当圆柱的底面半径为时，它的侧面积最大为π.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
