题目内容
(本 小题满分14分)
小题满分14分)
如右图所示,四棱锥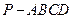 中,底面
中,底面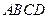 为正方形,
为正方形,
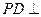 平面
平面 ,
,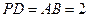 ,
,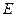 ,
,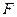 ,
,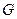 分别为
分别为
 、
、 、
、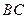 的中点.(1)求证:
的中点.(1)求证: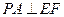 ;
;
(2)求二面角D-FG-E的余弦值.
 小题满分14分)
小题满分14分)如右图所示,四棱锥
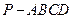 中,底面
中,底面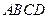 为正方形,
为正方形, 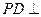 平面
平面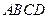 ,
,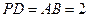 ,
,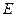 ,
,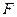 ,
,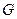 分别为
分别为
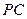 、
、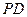 、
、 的中点.(1)求证:
的中点.(1)求证: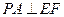 ;
;(2)求二面角D-FG-E的余弦值.

(1)证法1:∵
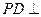 平面
平面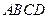 ,
,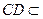 平面
平面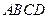 ,
,∴
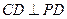 .
.又
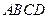 为正方形,
为正方形,∴
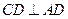 .
.∵
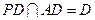 ,
,∴
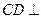 平面
平面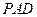 .…………………4分
.…………………4分∵
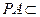 平面
平面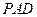 ,
,∴
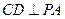 .
.∵
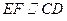 ,
,∴
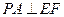 .…………………6分
.…………………6分证法2:以
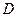 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系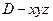 ,
,则
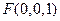 ,
,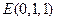 ,
,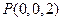 ,
,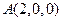 ,
,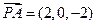 ,
,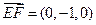 .…………………4分
.…………………4分∵
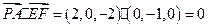 ,
,∴
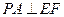 .…………………6分
.…………………6分(2)解法1:以
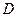 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系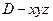 ,
,则
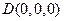 ,
,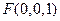 ,
,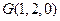 ,
,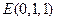 ,
,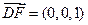 ,
,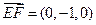 ,
,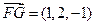 .…………………8分
.…………………8分设平面DFG的法向量为
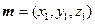 ,
,∵
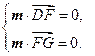
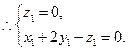
令
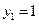 ,得
,得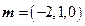 是平面
是平面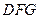 的一个法向量.…………10分
的一个法向量.…………10分设平面EFG的法向量为
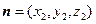 ,
,∵
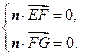
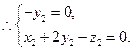
令
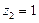 ,得
,得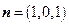 是平面
是平面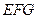 的一个法向量.……………12分
的一个法向量.……………12分∵
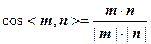
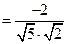
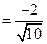
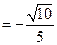 .
.设二面角
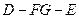 的平面角为θ,则
的平面角为θ,则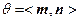 .
.所以二面
 角
角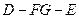 的余弦值为
的余弦值为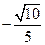 .…………………14分
.…………………14分解法2:以
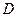 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系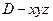 ,
,则
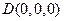 ,
,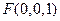 ,
,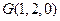 ,
,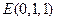 ,
,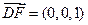 ,
,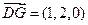 ,
,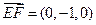 ,
,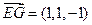 ,
,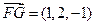 .…………………8分
.…………………8分 过
过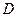 作
作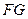 的垂线,垂足为
的垂线,垂足为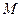 ,
,∵
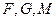 三点共线,
三点共线,∴
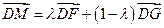 ,
,∵
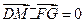 ,
,∴
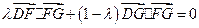 ,
,即
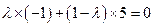 ,解得
,解得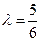 .…………………10分
.…………………10分∴
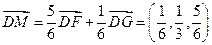 .
.再过
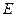 作
作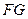 的垂线,垂足为
的垂线,垂足为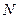 ,
,∵
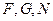 三点共线,∴
三点共线,∴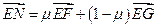 ,
,∵
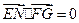 , ∴
, ∴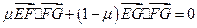 ,
,即
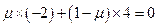 ,
,解得
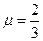 .∴
.∴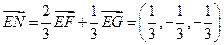 .
.∴
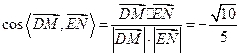 .…………………12分
.…………………12分∵
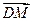 与
与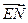 所成的角就是二面角
所成的角就是二面角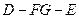 的平面角,
的平面角,所以二面角
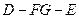 的余弦值为
的余弦值为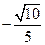 .…………………14分
.…………………14分略

练习册系列答案
相关题目
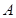 、
、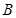 、
、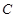 三点,
三点,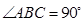 ,
,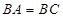 ,球心
,球心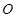 到平面
到平面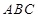 的距离是
的距离是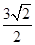 ,则
,则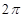
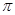
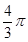
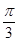
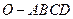 中,底面
中,底面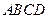 为菱形,
为菱形,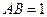 ,
,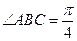 ,
,  ,
, 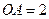 ,
,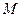 为
为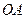 的中点,
的中点,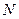 为
为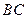 的中点
的中点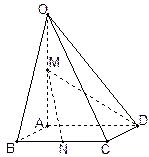
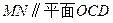
 ;
;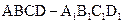 中,E是棱
中,E是棱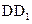 的中点.
的中点.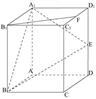
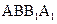 所成的角的正弦值;
所成的角的正弦值;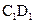 上是否存在一点F,使
上是否存在一点F,使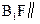 平面
平面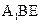 ?证明你的结论.
?证明你的结论. 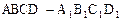 中,
中, AD=2,AB=AD=4,
AD=2,AB=AD=4,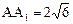 ,点E是AB的中点,点F是
,点E是AB的中点,点F是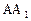 的中点。
的中点。 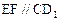 ;
; 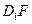 与
与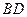
 所成的角的大小;
所成的角的大小;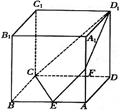
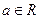 ,且以下命题都为真命题:
,且以下命题都为真命题: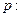 实系数一元二次方程
实系数一元二次方程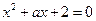 的两根都是虚数;
的两根都是虚数;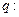 存在复数
存在复数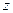 同时满足
同时满足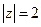 且
且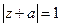 .
.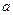 的取值范围.
的取值范围.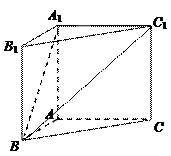
 a的
a的 值;
值; 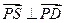 .
. 大值时,求异面直线AP与SD所成角的余弦值.
大值时,求异面直线AP与SD所成角的余弦值.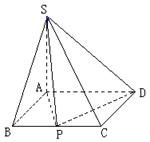
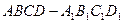 中,底面
中,底面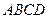 是
是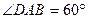
 的菱形,
的菱形,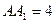 ,
,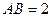 ,点
,点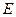 在棱
在棱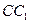 上,点
上,点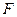 是棱
是棱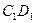 的中点.
的中点. ;
;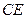 的长度,使得
的长度,使得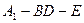 为直二面角.
为直二面角. B、
B、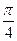 C、
C、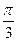 D、
D、