题目内容
(本小题满分12分)
如图,四棱锥S-ABCD的底面是矩形,AB=a,AD=2,SA=1,且SA⊥底面ABCD,若边BC上存在异于B,C的一点P,使得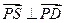 .
.
(1)求a的最大值;
(2)当a取最 大值时,求异面直线AP与SD所成角的余弦值.
大值时,求异面直线AP与SD所成角的余弦值.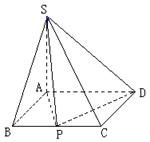
如图,四棱锥S-ABCD的底面是矩形,AB=a,AD=2,SA=1,且SA⊥底面ABCD,若边BC上存在异于B,C的一点P,使得
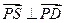 .
.(1)求a的最大值;
(2)当a取最
 大值时,求异面直线AP与SD所成角的余弦值.
大值时,求异面直线AP与SD所成角的余弦值.
解:建立如图所示的空间直角坐标系,则各点坐标分别为:
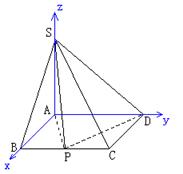 A(0, 0,0),B(a,0,0),C(a,2,0),D(0,2,0),S(0,0,1),设P(a,x,0),(0<x<2)
A(0, 0,0),B(a,0,0),C(a,2,0),D(0,2,0),S(0,0,1),设P(a,x,0),(0<x<2)(1) ∵
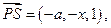
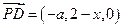 ………3分
………3分∴由
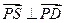 得: ×=0,
得: ×=0,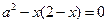
即:
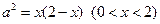
∴当且仅当x=1时,a有最大值为1.
此时P为BC中点;
 ………6分
………6分(2) 由(1)知:
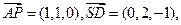 ………8分
………8分∴
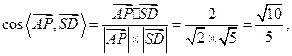 ………10分
………10分∴异面直线AP与SD所成角的余弦值为. ………12分
略

练习册系列答案
相关题目
 小题满分14分)
小题满分14分) 中,底面
中,底面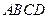 为正方形,
为正方形, 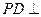 平面
平面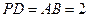 ,
,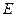 ,
,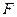 ,
,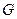 分别为
分别为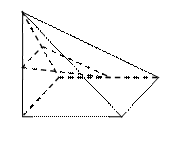
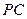 、
、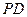 、
、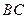 的中点.(1)求证:
的中点.(1)求证: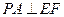 ;
;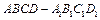 中,M、N、P、Q分别为AD、CD、
中,M、N、P、Q分别为AD、CD、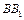 、
、 的中点.
的中点.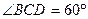 ,E是CD的中点,
,E是CD的中点,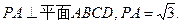
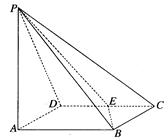
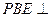 平面PAB;
平面PAB; 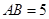 ,AA1=4,.点D是AB的中点.
,AA1=4,.点D是AB的中点.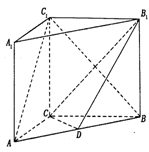
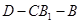 的平面角的正切值.
的平面角的正切值.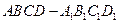 中,
中,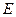 、
、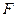 分别为
分别为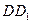 、
、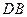 的
的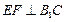 ;
;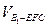 的体积.
的体积.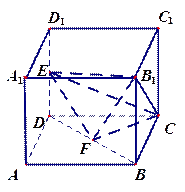
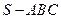 中,
中,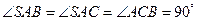 ,且
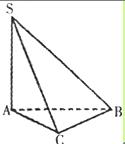
,且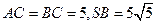 。
。
 ;
;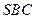 与底面
与底面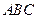 所成二面角的大小;
所成二面角的大小;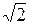 的正方形,E为P
的正方形,E为P C的中点,PB=PD.
C的中点,PB=PD.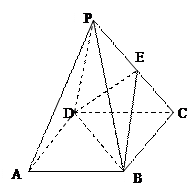
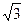 ,两个平面分别截球面得到两个圆⊙O1与⊙O2,若
,两个平面分别截球面得到两个圆⊙O1与⊙O2,若