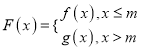题目内容
【题目】设函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 有两个极值点
有两个极值点![]() 且
且![]() ,求证
,求证![]() .
.
【答案】当![]() 时,函数
时,函数![]() 在
在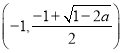 递减,在
递减,在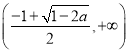 递增;当
递增;当![]() 时,函数
时,函数![]() 在
在 单调递增,在
单调递增,在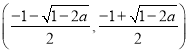 单调递减.
单调递减.
(Ⅱ)证明见解析
【解析】试题分析:(1)由函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,令
,令![]() ,则
,则![]() ,由根的判断式进行分类讨论,能求出函数
,由根的判断式进行分类讨论,能求出函数![]() 的单调区间;(2)由
的单调区间;(2)由![]() ,知函数
,知函数![]() 有两个极值点时,
有两个极值点时, ![]() ,由此推导出
,由此推导出![]() ,且
,且![]() ,即
,即![]() ,构造函数
,构造函数![]() ,能够证明
,能够证明![]() .
.
试题解析:(Ⅰ)定义域为![]()
![]()
令![]() ,则
,则![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() ,此时
,此时![]() ,故函数
,故函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() ,即
,即![]() 时,
时, ![]() 的两个根为
的两个根为
![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]()
故当![]() 时,函数
时,函数![]() 在
在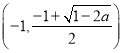 递减,在
递减,在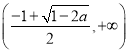 递增;当
递增;当![]() 时,函数
时,函数![]() 在
在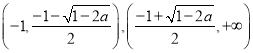 单调递增,在
单调递增,在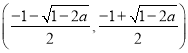 单调递减.
单调递减.
(Ⅱ)∵![]() ,∴当函数
,∴当函数![]() 有两个极值点时
有两个极值点时![]() ,
, ![]() ,
,
故此时![]() ,且
,且![]() ,即
,即![]() ,
, ![]() ,
,
设![]() ,其中
,其中![]() , 则
, 则![]() ,
,
由于![]() 时,
时, ![]() ,故函数
,故函数![]() 在
在![]() 上单调递增,
上单调递增,
故![]() .∴
.∴![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目