题目内容
【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:
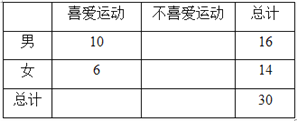
(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.
(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: 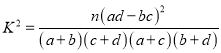
参考数据:

【答案】(1)不能;(2)![]() .
.
【解析】试题分析:
本题主要考查独立性检验及其应用、离散型随机变量的分布列与期望.(1)由题意完成列联表,再将表中数据代入公式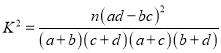 求出
求出![]() 观测值,对照概率表,即可得出结论;(2)由题意得
观测值,对照概率表,即可得出结论;(2)由题意得![]() 可取
可取![]() ,求出
,求出![]() 的每一个取值对应的概率,即可得出分布列与期望.
的每一个取值对应的概率,即可得出分布列与期望.
试题解析:
(1) 完成2×2列联表:

![]() .
.
![]()
![]() 在犯错误的概率不超过
在犯错误的概率不超过![]() 的前提下,不能判断喜爱运动与性别有关
的前提下,不能判断喜爱运动与性别有关![]()
(2)由题意得![]() 的所有可能取值有
的所有可能取值有![]()
![]() ;
;
![]() ;
;
![]() .
.
所以![]() 的分布列为
的分布列为
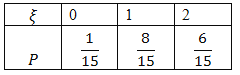
故![]() .
.

练习册系列答案
相关题目