题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,讨论函数
,讨论函数![]() 的零点的个数;
的零点的个数;
(3)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明:
,证明: ![]() .
.
【答案】(1)2x﹣y﹣1=0;(2)见解析;(3)见解析.
【解析】试题分析:(1)求出函数的导数,计算![]() ,求出切线方程即可;
,求出切线方程即可;
(Ⅱ)求出函数的导数,通过讨论![]() 的范围,根据函数的单调区间和函数的极值即可讨论函数
的范围,根据函数的单调区间和函数的极值即可讨论函数![]() 的零点的个数;;
的零点的个数;;
(Ⅲ)得到![]() 令
令![]() ,则
,则![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() ,证明结论即可.
,证明结论即可.
试题解析:
(1)当a=0时,f(x)= lnx+x,
则f(1)=1,所以切点为(1,1),
又f′(x)= ![]() +1,则切线斜率k = f′(1)=2,
+1,则切线斜率k = f′(1)=2,
故切线方程为:y﹣1=2(x﹣1),即2x﹣y﹣1=0
(2)g(x)=f(x)﹣(ax﹣1)=lnx﹣![]() ax2+(1﹣a)x+1,
ax2+(1﹣a)x+1,
所以g′(x)=![]() ﹣ax+(1﹣a)=
﹣ax+(1﹣a)=![]() ,
,
当a≤0时,因为x>0,所以g′(x)>0.
所以g(x)在(0,+∞)上是递增函数
而![]()
所以函数![]() 有且只有一个零点
有且只有一个零点
当0<a<1时,g′(x)=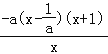 ,
,
令g′(x)=0,得x=![]() ,
,
所以当x∈(0,![]() )时,g′(x)>0;当x∈(
)时,g′(x)>0;当x∈(![]() ,+∞)时,g′(x)<0,
,+∞)时,g′(x)<0,
因此函数g(x)在x∈(0,![]() )是增函数,在(
)是增函数,在(![]() ,+∞)是减函数,
,+∞)是减函数,
∴x=![]() 时,g(x)有极大值g(
时,g(x)有极大值g(![]() )=
)=![]() ﹣lna>0
﹣lna>0
又![]()
∴当0<a<1时函数![]() 有两个零点
有两个零点
(3)证明:当![]()
所以![]()
即为: ![]()
所以![]()
令![]()
![]()
所以![]()
所以![]()
所以![]()
因为![]()

练习册系列答案
相关题目