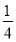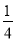题目内容
已知椭圆C: =1(a>b>0)的离心率为
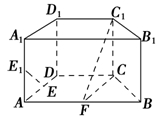
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足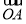 +
+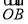 =t
=t (O为坐标原点),当|
(O为坐标原点),当|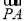 -
-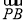 |<
|<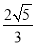 时,求实数t的取值范围.
时,求实数t的取值范围.
(1)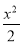 +y2=1.(2)
+y2=1.(2)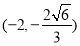 ∪
∪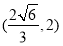
【解析】(1)由题意知椭圆的离心率e=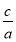 =
=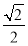 ,∴e2=
,∴e2=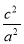 =
=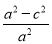 =
=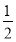 ,
,
即a2=2b2.
又△EGF2的周长为4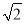 ,即4a=4
,即4a=4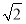 ,∴a2=2,b2=1.
,∴a2=2,b2=1.
∴椭圆C的方程为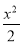 +y2=1.
+y2=1.
(2)由题意知直线AB的斜率存在,即t≠0.
设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),P(x,y),由 ,
,
得(1+2k2)x2-8k2x+8k2-2=0.
由Δ=64k4-4(2k2+1)(8k2-2)>0,得k2<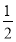 .x1+x2=
.x1+x2=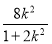 ,x1x2=
,x1x2=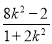 ,
,
∵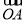 +
+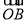 =t
=t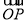 ,
,
∴(x1+x2,y1+y2)=t(x,y),x=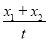 =
=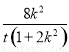 ,y=
,y=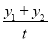 =
=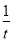 [k(x1+x2)-4k]=
[k(x1+x2)-4k]=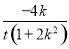 .
.
∵点P在椭圆C上,
∴ +2
+2 =2,
=2,
∴16k2=t2(1+2k2).
∵|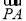 -
-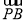 |<
|<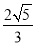 ,∴
,∴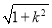 |x1-x2|<
|x1-x2|<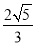 ,
,
∴(1+k2)[(x1+x2)2-4x1x2]<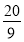 ,
,
∴(1+k2)  <
<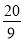 ,
,
∴(4k2-1)(14k2+13)>0,
∴k2>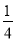 .∴
.∴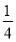 <k2<
<k2<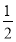 .
.
∵16k2=t2(1+2k2),∴t2=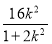 =8-
=8-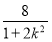 ,
,
又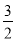 <1+2k2<2,∴
<1+2k2<2,∴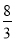 <t2=8-
<t2=8-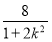 <4,
<4,
∴-2<t<- 或
或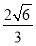 <t<2,
<t<2,
∴实数t的取值范围为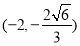 ∪
∪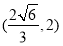

练习册系列答案
相关题目