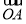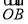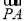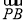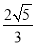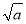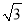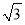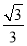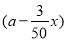题目内容
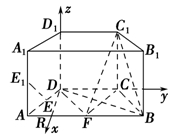
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
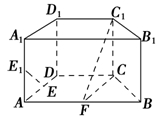
(1)证明:直线EE1∥平面FCC1;
(2)求二面角B-FC1-C的余弦值.
(1)见解析(2)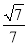
【解析】(1)证明
法一 取A1B1的中点F1,连接FF1,C1F1,由于FF1∥BB1∥CC1,
所以F1∈平面FCC1,
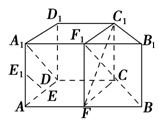
因此平面FCC1,即为平面C1CFF1.,连接A1D,F1C,由于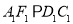
 CD,
CD,
所以四边形A1DCF1为平行四边形,因此A1D∥F1C.又EE1∥A1D,得EE1∥F1C.
而EE1?平面FCC1,F1C?平面FCC1,故EE1∥平面FCC1.
法二 因为F为AB的中点,CD=2,AB=4,AB∥CD,所以CD  AF.
AF.
因此四边形AFCD为平行四边形,所以AD∥FC.
又CC1∥DD1,FC∩CC1=C,FC?平面FCC1,CC1?平面FCC1,
所以平面ADD1A1∥平面FCC1.又EE1?平面ADD1A1,所以EE1∥平面FCC1.
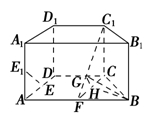
(2)解 法一 取FC的中点H,由于FC=BC=FB,所以BH⊥FC.又BH⊥CC1,CC1∩FC=C.所以BH⊥平面FCC1.过H作HG⊥C1F于G,连接BG.由于HG⊥C1F,BH⊥平面FCC1,所以C1F⊥平面BHG.因此BG⊥C1F,所以∠BGH为所求二面角的平面角.在Rt△BHG中,BH=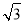 ,
,
又FH=1,且△FCC1为等腰直角三角形,所以HG=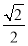 ,BG=
,BG= =
=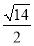 ,因此cos∠BGH=
,因此cos∠BGH=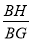 =
=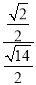 =,
=,
即所求二面角的余弦值为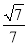 .
.
法二 过D作DR⊥CD交AB于R,以D为坐标原点建立如图所示的空间直角坐标系,则F(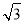 ,1,0),B(
,1,0),B(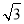 ,3,0),C(0,2,0),C1(0,2,2).
,3,0),C(0,2,0),C1(0,2,2).
所以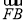 =(0,2,0),
=(0,2,0),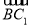 =(-
=(- ,-1,2),
,-1,2), =(
=(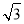 ,3,0).
,3,0).
由FB=CB=CD=DF,所以DB⊥FC.又CC1⊥平面ABCD,
所以 为平面FCC1的一个法向量.
为平面FCC1的一个法向量.
设平面BFC1的一个法向量为n=(x,y,z),
则由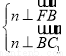 得
得 即
即 取x=1,得
取x=1,得
因此n=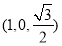 ,所以cos〈
,所以cos〈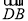 ,n〉=
,n〉= =
=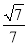 .
.
故所求二面角的余弦值为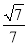 .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案