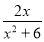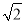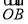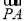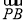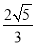Question

已知函数f(x)＝sin (2x＋φ)，其中φ为实数，若f(x)≤ 对x∈R恒成立，且<f(π)，则下列结论正确的是(　　)．

A．＝－1

B．f>f

C．f(x)是奇函数

D．f(x)的单调递增区间是 (k∈Z)

 

Answer 1

D

【解析】由f(x)≤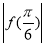 恒成立知x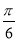＝是函数的对称轴，即2×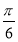＋φ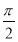＝＋kπ，k∈Z，所以φ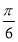＝＋kπ，k∈Z，又f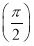<f(π)，所以sin (π＋φ)<sin (2π＋φ)，即－sin φ<sin φ.所以sin φ>0，得φ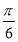＝，即f(x)＝sin 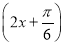，由－＋2kπ≤2x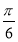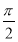＋≤＋2kπ，k∈Z，得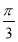－＋kπ≤x≤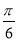＋kπ，k∈Z，即函数的单调递增区间是 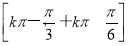(k∈Z)．