Question

【题目】已知二次函数（a,b为常数）满足条件，且方程有两个相等的实数根.

（1）求的解析式；

（2）是否存在实数（m<n）,使得的定义域和值域分别为，如果存在，求出。不存在，说明理由。

Answer 1

【答案】（1）（2）

【解析】试题分析：（1）由条件，得二次函数对称轴，再根据方程有两个相等的实数根得判别式为零，解方程组得a,b值（2）先确定函数值域得最大值为，因此可得范围，进而可得定义区间与对称轴位置关系，确定对应单调关系，得有两个不等实根，求出

试题解析：解：（）由方程有两个相等的实数根

得(b-2)2 =0,则b=2,.

由知对称轴方程为,

则

(2) 存在.由即，

而抛物线的对称轴为x=1，则时，

在[m,n]上为增函数.

假设满足题设条件的m,n存在，

则即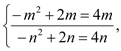

解得

又m＜n,所以存在