题目内容
【题目】若函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)写出函数f(x)(x∈R)的解析式.
(2)若函数g(x)=f(x)+(4﹣2a)x+2(x∈[1,2]),求函数g(x)的最小值h(a).
【答案】
(1)解:设x>0,则﹣x<0.又因为当x≤0时,f(x)=x2+2x,
所以f(﹣x)=(﹣x)2+2(﹣x)=x2﹣2x,又因为f(﹣x)=f(x).
所以x>0时,f(x)=x2﹣2x.
所以f(x)= ![]()
(2)解:函数g(x)=f(x)+(4﹣2a)x+2(x∈[1,2]),f(x)= ![]() .
.
∴g(x)=x2+2(1﹣a)x+2.x∈[1,2],
①当a﹣1≤1时,即a≤2,g(x)min=g(1)=5﹣2a
②当1<a﹣1<2时,即2<a<3,g(x)min=g(a﹣1)=﹣a2+2a+1
③当a﹣1≥2时,即a≥3,g(x)min=g(2)=10﹣4a
综上:h(a)= 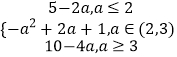
【解析】(1)利用函数的奇偶性曲线函数的解析式即可.(2)利用分段函数以及二次函数的性质,通过分类讨论求解函数的最小值即可.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值),还要掌握函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇)的相关知识才是答题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目