题目内容
【题目】在平面直角坐标系
中，点M到点
的距离比它到
轴的距离大2，记点M的轨迹为C．
（1）求轨迹C的方程；
（2）若直线
与轨迹C恰有2个公共点，求实数b的取值范围．
【答案】（1）
；（2）
【解析】
（1）设
，根据动点
满足的几何性质得到
，化简后可得轨迹方程．
（2）轨迹
由抛物线和射线构成，故直线
与抛物线有两个交点或与抛物线、射线各有一个交点，联立直线方程和抛物线线方程后利用判别式可求
的取值范围．
（1）设轨迹上的动点，则由题意，，∴
，∴轨迹的方程为．
（2）轨迹与直线有两个交点，等价于
①直线与
，
各有一个交点或
②直线与有两个交点，且与没有交点，
由
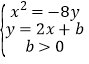得
，
由①得此方程有两个相等的根即
，∴
．
由②得：当
时，方程有两个不等非正根，
故 
，∴，
∴直线与轨迹恰有二个公共点时的范围是
阅读快车系列答案
【题目】2017年春晚分会场之一是凉山西昌，电视播出后，通过网络对凉山分会场的表演进行了调查．调查分三类人群进行，参加了网络调查的观众们的看法情况如下：
观众对凉山分会场表演的看法 | 非常好 | 好 |
中国人且非四川（人数比例） |
|
|
四川人（非凉山）（人数比例） |
|
|
凉山人（人数比例） |
|
|
（1）从这三类人群中各选一个人，求恰好有2人认为“非常好”的概率（用比例作为相应概率）；
（2）若在四川人（非凉山）群中按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为“非常好”的人数记为ξ，求ξ的分布列和数学期望．
【题目】对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组 | 频数 | 频率 |
[10，15） | 10 | 0.25 |
[15，20） | 25 | n |
[20，25） | m | p |
[25，30） | 2 | 0.05 |
合计 | M | 1 |
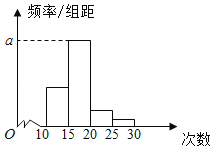
（1）求出表中M，p及图中a的值；
（2）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，请列举出所有基本事件，并求至多1人参加社区服务次数在区间[20，25）内的概率．
【题目】张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表：
年龄 （岁） | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 （cm） | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
（Ⅰ）求身高y关于年龄x的线性回归方程；
（Ⅱ）利用（Ⅰ）中的线性回归方程，分析张三同学7岁至13岁身高的变化情况，如17岁之前都符合这一变化，请预测张三同学15岁时的身高．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
= 
， 
．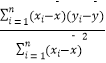