题目内容
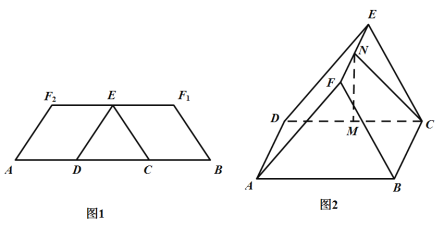
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
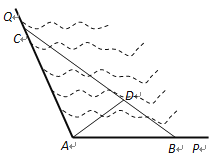
【答案】(1)![]() 和AC的长度分别为750米和1500米(2)
和AC的长度分别为750米和1500米(2)![]() 万元
万元
【解析】
试题(1)设![]() 长为
长为![]() 米,
米,![]() 长为
长为![]() 米,依题意得
米,依题意得![]() ,即
,即![]() ,表示面积,利用基本不等式可得结论;(2)利用向量方法,将
,表示面积,利用基本不等式可得结论;(2)利用向量方法,将![]() 表示为
表示为![]() ,根据向量的数量积与模长的关系可得结果.
,根据向量的数量积与模长的关系可得结果.
试题解析:(1)设![]() 长为
长为![]() 米,
米,![]() 长为
长为![]() 米,依题意得
米,依题意得![]() ,
,
即![]() ,
,
![]()
![]()
![]()
![]() =
=![]()
![]()
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
所以当![]() 的面积最大时,
的面积最大时,![]() 和AC的长度分别为750米和1500米
和AC的长度分别为750米和1500米
(2)在(1)的条件下,因为![]() .
.
由![]()
得![]()
![]()
![]()
![]()
![]() ,
,
![]() 元
元
所以,建水上通道![]() 还需要
还需要![]() 万元.
万元.
解法二:在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
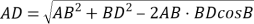
![]()
在![]() 中,
中,![]()
![]() =
=![]()
![]() 元
元
所以,建水上通道![]() 还需要
还需要![]() 万元.
万元.
解法三:以A为原点,以AB为![]() 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则![]() ,
,![]()
![]() ,即
,即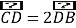 ,设
,设![]()
由![]() ,求得
,求得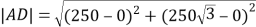 , 所以
, 所以![]()
所以,![]()
![]()
![]() 元
元
所以,建水上通道![]() 还需要
还需要![]() 万元.
万元.

 名校课堂系列答案
名校课堂系列答案【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.