题目内容
4．已知数列{an}满足an+1=$\frac{{a}_{n}}{{2}_{{a}_{n}+1}}$，a1=1（n∈N+）（1）计算a2，a3，a4，a5；
（2）猜想{an}的通项公式并用数学归纳法证明．
分析 （1）由数列{an}的递推公式依次求出a2，a3，a4，a5；
（2）根据a2，a3，a4，a5值的结构特点猜想{an}的通项公式，再用数学归纳法①验证n=1成立，②假设n=k时命题成立，证明当n=k+1时命题也成立
解答 解：（1）计算得a2=$\frac{1}{3}$，a3=$\frac{1}{5}$，a4=$\frac{1}{7}$，a5=$\frac{1}{9}$；
（2）猜想an=$\frac{1}{2n-1}$
下面用数学归纳法证明这个猜想．①当n=1时，a1=1，命题成立．
②假设n=k时命题成立，即ak=$\frac{1}{2k-1}$成立，
那么，当n=k+1时，ak+1=$\frac{{a}_{k}}{2{a}_{k}+1}$=$\frac{\frac{1}{2k-1}}{2×\frac{1}{2k-1}+1}$=$\frac{1}{2k+1}$=$\frac{1}{2（k+1）-1}$，
由①②知命题对一切n∈N*均成立．
点评 本题考查数列递推关系式的应用，数学归纳法证明数列问题的方法，考查逻辑推理能力，计算能力．注意在证明n=k+1时用上假设，化为n=k的形式，属于中档题．
练习册系列答案
相关题目
12．如图所示，程序执行后的输出结果为（ ）
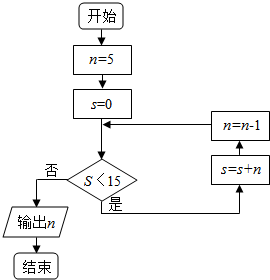
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
19．命题“$?x∈[{\frac{π}{2}，π}]，sinx-cosx＞2$”的否定是（ ）
| A． | $?x∈[{\frac{π}{2}，π}]，sinx-cosx＜2$ | B． | $?x∈[{\frac{π}{2}，π}]，sinx-cosx≤2$ | ||
| C． | $?x∈[{\frac{π}{2}，π}]，sinx-cosx≤2$． | D． | $?x∈[{\frac{π}{2}，π}]，sinx-cosx＜2$ |
16．用数学归纳法证明对任意正整数n，都有$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$＞$\frac{13}{24}$的过程中，由n=k推导n=k+1时，不等式的左边增加的式子为（ ）
| A． | $\frac{1}{2k+2}$ | B． | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$ | C． | $\frac{1}{2k+1}$-$\frac{1}{2k+2}$ | D． | $\frac{1}{2k+1}$-$\frac{3}{2k+2}$ |
13．已知实数x，y满足不等式组$\left\{{\begin{array}{l}{2x-y+2≥0}\\{x+y-2≥0}\\{x≤2}\end{array}}\right.$，则$\frac{y-1}{x+3}$的取值范围是（ ）
| A． | $（-∞，-\frac{1}{5}]∪[1，+∞）$ | B． | $[\frac{1}{3}，1]$ | C． | [-$\frac{1}{5}$，$\frac{1}{3}$] | D． | [-$\frac{1}{5}$，1] |