题目内容
【题目】如图所示,已知多面体![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() 底面
底面![]() ,
,![]() 且
且![]() .
.
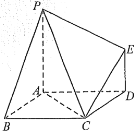
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)先证明平面![]() 平面
平面![]() ,即可得证线面平行;
,即可得证线面平行;
(2)取PA的中点M,连接MD,MC,根据余弦定理求解![]() 即可得解.
即可得解.
(1)由题![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
四边形![]() 是边长为2的菱形,所以
是边长为2的菱形,所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面
![]() ,所以
,所以![]() 平面
平面![]() ,CD和DE是平面CDE内两条相交直线,
,CD和DE是平面CDE内两条相交直线,
所以平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)取PA的中点M,连接MD,MC,由题可得![]() ,
,
所以四边形PMDE是平行四边形,所以PE∥MD,又![]() ,
,
异面直线![]() 与
与![]() 所成角就是MD与CD所成角,
所成角就是MD与CD所成角,
![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,所以三角形ABC是等边三角形,
,所以三角形ABC是等边三角形,
![]() 底面
底面![]() ,
,![]() ,
,
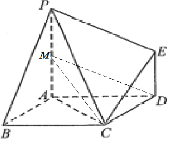
在三角形MDC中,由余弦定理![]() ,
,
所以异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目