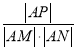题目内容
【题目】已知椭圆C:![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() ,左顶点为A,过点A的直线l与C交于另一个点M,且与直线x=t交于点N.
,左顶点为A,过点A的直线l与C交于另一个点M,且与直线x=t交于点N.
(1)求椭圆C的方程;
(2)是否存在实数t,使得![]() 为定值?若存在,求实数t的值;若不存在,请说明理由.
为定值?若存在,求实数t的值;若不存在,请说明理由.
【答案】(1)![]() y2=1;(2)存在,t
y2=1;(2)存在,t![]()
【解析】
(1)由题意可得b=1,运用椭圆的离心率公式和a,b,c的关系,可得a,c,进而得到椭圆方程;
(2)假设存在实数t=t0,使得![]() 为定值.可设直线l的方程为y=k(x+2),M(x0,y0),联立椭圆的方程,运用韦达定理,求得M的坐标,将t=t0代入y=k(x+2),求得N的坐标,再由向量的数量积的坐标表示,结合定值,可得所求值.
为定值.可设直线l的方程为y=k(x+2),M(x0,y0),联立椭圆的方程,运用韦达定理,求得M的坐标,将t=t0代入y=k(x+2),求得N的坐标,再由向量的数量积的坐标表示,结合定值,可得所求值.
(1)由题意可得2b=2,即b=1,e![]() ,a2﹣b2=c2,
,a2﹣b2=c2,
解得a=2,c![]() ,则椭圆C的方程为
,则椭圆C的方程为![]() y2=1;
y2=1;
(2)假设存在实数t=t0,使得![]() 为定值.
为定值.
由题意可得直线l的斜率存在,由A(﹣2,0),可设直线l的方程为y=k(x+2),M(x0,y0),
联立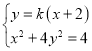 ,可得(1+4k2)x2+16k2x+16k2﹣4=0,
,可得(1+4k2)x2+16k2x+16k2﹣4=0,
由韦达定理可得﹣2x0![]() ,即x0
,即x0![]() ,y0=k(x0+2)
,y0=k(x0+2)![]() ,
,
即M(![]() ,
,![]() ),
),
将t=t0代入y=k(x+2),可得N(t0,k(t0+2)),
则![]()
![]() ,
,
若![]() 为定值,则
为定值,则![]() ,
,
span>解得t0![]() ,此时
,此时![]() 为定值
为定值![]() ,
,
所以存在实数t![]() ,使得
,使得![]() 为定值
为定值![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目