题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为![]() ,且
,且![]() 与短轴两端点的连线相互垂直.
与短轴两端点的连线相互垂直.
(1)求椭圆![]() 的方程;
的方程;
(2)若圆![]() 上存在两点
上存在两点![]() ,
,![]() ,椭圆
,椭圆![]() 上存在两个点
上存在两个点![]() 满足:
满足:![]() 三点共线,
三点共线,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)又题意知,![]() ,
,![]() 及
及![]() 即可求得
即可求得![]() ,从而得椭圆方程.
,从而得椭圆方程.
(2)分三种情况:直线![]() 斜率不存在时,
斜率不存在时,![]() 的斜率为0时,
的斜率为0时,![]() 的斜率存在且不为0时,设出直线方程,联立方程组,用韦达定理和弦长公式以及四边形的面积公式计算即可.
的斜率存在且不为0时,设出直线方程,联立方程组,用韦达定理和弦长公式以及四边形的面积公式计算即可.
(1)由焦点与短轴两端点的连线相互垂直及椭圆的对称性可知,![]() ,
,
∵过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为![]() .
.![]()
又![]() ,解得
,解得![]() .
.
∴椭圆![]() 的方程为
的方程为![]()
(2)由(1)可知圆![]() 的方程为
的方程为![]() ,
,
(i)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的斜率为0,
的斜率为0,
此时![]()
(ii)当直线![]() 的斜率为零时,
的斜率为零时,![]() .
.
(iii)当直线![]() 的斜率存在且不等于零时,设直线
的斜率存在且不等于零时,设直线![]() 的方程为
的方程为![]() ,
,
联立![]() ,得
,得![]() ,
,
设![]() 的横坐标分别为
的横坐标分别为![]() ,则
,则![]() .
.
所以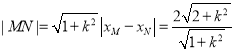 ,
,
(注:![]() 的长度也可以用点到直线的距离和勾股定理计算.)
的长度也可以用点到直线的距离和勾股定理计算.)
由![]() 可得直线
可得直线![]() 的方程为
的方程为![]() ,联立椭圆
,联立椭圆![]() 的方程消去
的方程消去![]() ,
,
得![]()
设![]() 的横坐标为
的横坐标为![]() ,则
,则![]() .
.
![]()
![]()
![]() .
.
综上,由(i)(ii)(ⅲ)得![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目