题目内容
4.若函数f(x)=-x2+2ax-3与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则实数a的取值范围是( )| A. | (-1,0) | B. | (-1,0)∪(0,1] | C. | (0,1) | D. | (0,1] |
分析 若函数f(x)=-x2+2ax-3与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则$\left\{\begin{array}{l}a≤1\\ a+1>1\end{array}\right.$,解得答案.
解答 解:∵函数f(x)=-x2+2ax-3与g(x)=(a+1)1-x在区间[1,2]上都是减函数,
∴$\left\{\begin{array}{l}a≤1\\ a+1>1\end{array}\right.$,
解得:a∈(0,1],
故答案为:D
点评 本题考查的知识点是指数函数的图象和性质,二次函数的图象和性质,复合函数的单调性,难度中档.

练习册系列答案
相关题目
12.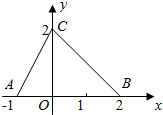 如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )
如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )
 如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )
如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )| A. | {x|-1<x≤0} | B. | {x|-1≤x≤1} | C. | {x|-1≤x<1} | D. | {x|-1<x≤2} |
13.圆x2+y2-2x+4y=0与2tx-y-2-2t=0(t∈R)的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 以上都有可能 |