题目内容
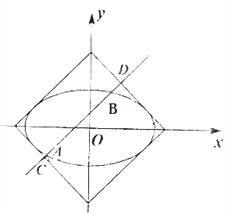
【题目】如图,曲线![]() 与正方形
与正方形![]() :
: ![]() 的边界相切.
的边界相切.
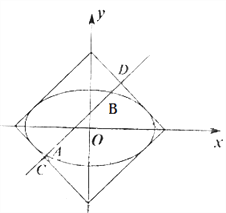
(1)求![]() 的值;
的值;
(2)设直线![]() 交曲线
交曲线![]() 于
于![]() ,交
,交![]() 于
于![]() ,是否存在这样的曲线
,是否存在这样的曲线![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() 成等差数列?若存在,求出实数
成等差数列?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)由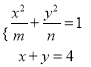 ,得(n+m)x2﹣8mx+16m﹣mn=0,由此利用韦达定理能求出m+n;(2)若|CA|,|AB|,|BD|成等差数列,则|AB|=
,得(n+m)x2﹣8mx+16m﹣mn=0,由此利用韦达定理能求出m+n;(2)若|CA|,|AB|,|BD|成等差数列,则|AB|=![]() ,由
,由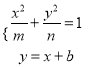 ,得(n+m)x2+2bmx+mb2﹣mn=0.由此利用根的判别式、韦达定理、弦长公式,结合已知条件能求出结果.
,得(n+m)x2+2bmx+mb2﹣mn=0.由此利用根的判别式、韦达定理、弦长公式,结合已知条件能求出结果.
解析:
(Ⅰ)由题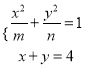 ,得
,得![]() ,
,
有⊿=![]() ,
,
化简的![]() .
.
又![]() ,所以
,所以![]() 从而有
从而有![]() ;
;
(Ⅱ)由![]() ,
,
![]() ,即
,即![]()
由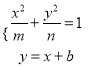 ,
, ![]()
由![]() 可得
可得![]() 且
且![]() ,
, ![]()
所以
可得![]() ,
,
从而![]()
所以![]() ,即有
,即有![]() ,符合
,符合![]() , 故当实数
, 故当实数![]() 的取值范围是
的取值范围是![]() 时,存在直线
时,存在直线![]() 和曲线
和曲线![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() 成等差数列
成等差数列

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,记这3人中“微信控”的人数为![]() ,试求
,试求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |