题目内容
【题目】选修4-4:坐标系与参数方程
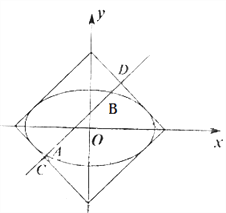
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() :
: ![]() ,C:
,C: ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)消参得到直线的普通方程,对于曲线![]() ,
, ![]() ,再利用
,再利用![]() 化解为曲线的直角坐标方程;(2)将直线的参数方程代入曲线C的普通方程,得到
化解为曲线的直角坐标方程;(2)将直线的参数方程代入曲线C的普通方程,得到![]() ,根据
,根据![]() ,根据根与系数的关系得到弦长,再计算点到直线的距离,从而求得三角形的面积.
,根据根与系数的关系得到弦长,再计算点到直线的距离,从而求得三角形的面积.
试题解析:(1)![]() 直线
直线![]() 的参数方程为
的参数方程为![]() ,①+②得
,①+②得![]() ,故
,故![]() 的普通方程为
的普通方程为![]() .
.
又曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即9
,即9![]() ,
,
![]() .
. ![]() ,即
,即![]() ,
,
(2)![]() 点
点![]() 的极坐标为
的极坐标为![]() ,
, ![]() 的直角坐标为(-1,1).
的直角坐标为(-1,1). ![]() 点
点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
将![]() ,代入
,代入![]() 中得
中得![]() .
.
设交点![]() 、
、![]() 对应的参数值分别为
对应的参数值分别为![]() ,则
,则![]() ,
, ![]() .
.
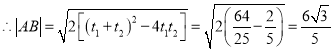
![]() 的面积
的面积![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市公交公司为了鼓励广大市民绿色出行,计划在某个地段增设一个起点站,为了研究车辆发车的间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
间隔时间( | 8 | 10 | 12 | 14 | 16 |
等候人数( | 16 | 19 | 23 | 26 | 29 |
调查小组先从这5组数据中选取其中的4组数据求得线性回归方程,再用剩下的1组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
(1)若选取的是前4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断所求方程是否是“理想回归方程”;
,并判断所求方程是否是“理想回归方程”;
(2)为了使等候的乘客不超过38人,试用所求方程估计间隔时间最多可以设为多少分钟?
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
 ,
,![]() .
.
【题目】某公司为了确定下一年度投入某种产品的宣传费用,需了解年宣传费![]() (单位:万元)对年销量
(单位:万元)对年销量![]() (单位:吨)和年利润(单位:万元)的影响.对近6年宣传费
(单位:吨)和年利润(单位:万元)的影响.对近6年宣传费![]() 和年销量
和年销量![]() 的数据做了初步统计,得到如下数据:
的数据做了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() 即
即![]() ,对上述数据作了初步处理,得到相关的值如下表:
,对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)从表中所给出的6年年销售量数据中任选2年做年销售量的调研,求所选数据中至多有一年年销售量低于20吨的概率.
(Ⅱ)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)若生产该产品的固定成本为200(万元),且每生产1(吨)产品的生产成本为20(万元)(总成本=固定成本+生产成本+年宣传费),销售收入为![]() (万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入
(万元),假定该产品产销平衡(即生产的产品都能卖掉),2019年该公司计划投入![]() 万元宣传费,你认为该决策合理吗?请说明理由.(其中
万元宣传费,你认为该决策合理吗?请说明理由.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为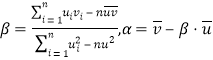 .
.