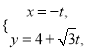题目内容
【题目】在如图所示的几何体中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,二面角
,二面角![]() 的大小为
的大小为![]() .
.
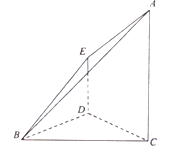
(1)求证: ![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的角(锐角)的大小;
所成的角(锐角)的大小;
(3)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(Ⅰ)由已知可得AC⊥CD,AC⊥CB,即∠BCD为二面角B﹣AC﹣E的平面角,即∠BCD=60°,求解三角形可得BD⊥DC,再由线面垂直的判定可得AC⊥平面BCD,得到AC⊥BD,进一步得到BD⊥平面ACDE;
(Ⅱ)由BD⊥平面ACDE,得BD⊥DC,BD⊥DE,可得DB,DC,DE两两垂直,分别以DB,DC,DE所在直线为x,y,z轴建立空间直角坐标系,求出所用点的坐标,得到平面BAE与平面BCD的一个法向量,由两法向量所成角的余弦值可得平面BCD与平面BAE所成的角;
(Ⅲ)若F为AB的中点,由(II)可得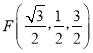 ,进一步得到
,进一步得到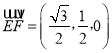 ,由已知可得平面BDE的一个法向量为
,由已知可得平面BDE的一个法向量为![]() ,由
,由![]() 与
与![]() 所成角的余弦值的绝对值可得直线EF与平面BDE所成角的大小.
所成角的余弦值的绝对值可得直线EF与平面BDE所成角的大小.
试题解析:
(1)因为![]() ,则
,则![]() ,
, ![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
由![]() ,
, ![]() ,且
,且![]() ,可知
,可知![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由![]() 平面
平面![]() 得
得![]() ,
, ![]() ,又
,又![]() ,即
,即![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
则以![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系,如图所示.
轴的正方向建立空间直角坐标系,如图所示.
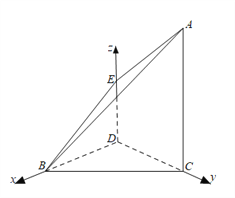
由(I)知![]() , 则
, 则![]() ,
, ![]() ,
, ![]() ,
,
由![]() 得
得![]() ,
, ![]()
依题意![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,即
,即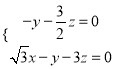 ,不妨设
,不妨设![]() ,可得
,可得![]() ,
,
由![]() 平面
平面![]() 可知平面
可知平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 与平面
与平面![]() 所成的角(锐角)为
所成的角(锐角)为![]() ,
,
所以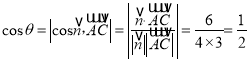 ,于是
,于是![]() ,
,
所以平面![]() 与平面
与平面![]() 所成的角(锐角)为
所成的角(锐角)为![]() .
.
(3)若![]() 为
为![]() 的中点,则由(II)可得
的中点,则由(II)可得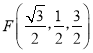 ,所以
,所以 ,
,
依题意![]() 平面
平面![]() ,可知平面
,可知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
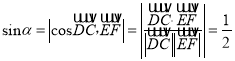 ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() .
.