题目内容
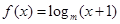 ,
,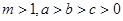 ,则
,则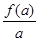 ,
,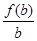 ,
,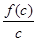 从小到大的顺序为 。
从小到大的顺序为 。
试题分析:∵m>1,∴函数
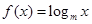 为增函数,
为增函数,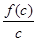 -
-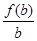 =
=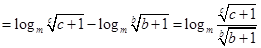 ,又b>c>0,∴
,又b>c>0,∴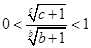 ,∴
,∴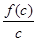 -
-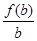 <0即
<0即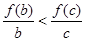 ,同理
,同理 ,∴
,∴
点评:此类问题常常利用作差法进行比较大小,同时考查了对数运算和对数函数的单调性,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
题目内容
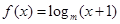 ,
,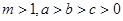 ,则
,则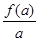 ,
,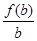 ,
,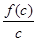 从小到大的顺序为 。
从小到大的顺序为 。
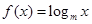 为增函数,
为增函数,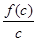 -
-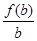 =
=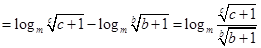 ,又b>c>0,∴
,又b>c>0,∴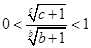 ,∴
,∴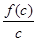 -
-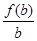 <0即
<0即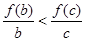 ,同理
,同理 ,∴
,∴

 科学实验活动册系列答案
科学实验活动册系列答案