题目内容
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x.
(1)求f(π)的值;
(2)当-4≤x≤4时,求f(x)的图象与x轴所围成图形的面积;
(3)写出(-∞,+∞)内函数f(x)的单调区间.
(1)求f(π)的值;
(2)当-4≤x≤4时,求f(x)的图象与x轴所围成图形的面积;
(3)写出(-∞,+∞)内函数f(x)的单调区间.
(1)π-4.
(2)4
(3)递增区间为[4k-1,4k+1](k∈Z),单调递减区间[4k+1,4k+3](k∈Z)
(2)4
(3)递增区间为[4k-1,4k+1](k∈Z),单调递减区间[4k+1,4k+3](k∈Z)
试题分析:解:(1)由f(x+2)=-f(x)得,
f(x+4)=f[(x+2)+2]=-f(x+2)=f(x),
所以f(x)是以4为周期的周期函数,
∴f(π)=f(-1×4+π)=f(π-4)=-f(4-π)=-(4-π)=π-4.
(2)由f(x)是奇函数与f(x+2)=-f(x),得:f[(x-1)+2]=-f(x-1)=f[-(x-1)],即f(1+x)=f(1-x).
故知函数y=f(x)的图象关于直线x=1对称.
又0≤x≤1时,f(x)=x,且f(x)的图象关于原点成中心对称,则f(x)的图象如图所示.

当-4≤x≤4时,f(x)的图象与x轴围成的图形面积为S,则
S=4S△OAB=4×
 =4.
=4.(3)根据(1)(2)可知函数的图形,根据奇偶性以及解析式和对称中心可知,

在一个周期[-1,3]内的图象可知增区间为[-1,1],减区间为[1,3],那么推广到整个实数域可知,都加上周期的整数倍即可,故可知函数f(x)的单调递增区间为[4k-1,4k+1](k∈Z),单调递减区间[4k+1,4k+3](k∈Z)
点评:主要是考查了函数的图象与性质的综合运用,属于中档题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
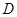 的函数
的函数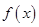 ,其导函数为
,其导函数为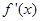 .若对
.若对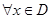 ,均有
,均有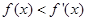 ,则称函数
,则称函数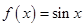 ,试判断
,试判断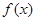 是否为其定义域上的梦想函数,并说明理由;
是否为其定义域上的梦想函数,并说明理由;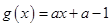 (
(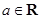 ,
,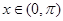 )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求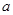 的取值范围;
的取值范围;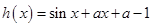 (
(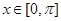 )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求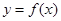 ,任取
,任取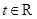 ,定义集合
,定义集合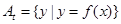 ,点
,点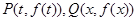 满足
满足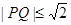 ,设
,设 ,
, 分别表示集合
分别表示集合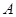 中元素的最大值和最小值,记
中元素的最大值和最小值,记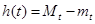 ,则
,则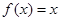 ,则
,则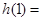 ;
;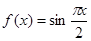 ,则
,则 的最小正周期为 .
的最小正周期为 .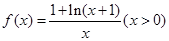 .
.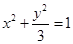 在
在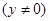
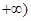 上单调性并证明你的结论;
上单调性并证明你的结论;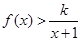 恒成立, 求整数
恒成立, 求整数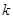 的最大值;
的最大值;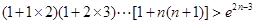 .
.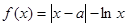
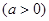 .
.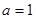 ,求
,求 的单调区间及
的单调区间及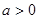 ,求
,求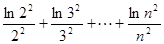 与
与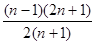 的大小
的大小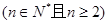 ,并证明你的结论.
,并证明你的结论.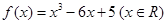 ,若关于
,若关于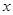 的方程
的方程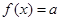 有三个不同实根,则
有三个不同实根,则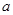 的取值范围是
的取值范围是 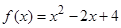 的单调减区间是 .
的单调减区间是 .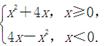 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )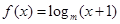 ,
,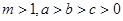 ,则
,则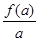 ,
,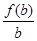 ,
,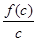 从小到大的顺序为 。
从小到大的顺序为 。