题目内容
函数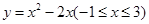 的值域是( )
的值域是( )
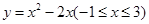 的值域是( )
的值域是( ) A.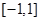 | B. | C.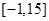 | D.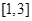 |
B
试题分析:因为函数
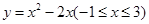 ,开口向上,对称轴x=1,那么在
,开口向上,对称轴x=1,那么在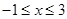 ,函数先递减在递增,可知函数的最小值为顶点的函数值-1,最大值在x=-1,x=3处取得,即为3,那么函数的值域为
,函数先递减在递增,可知函数的最小值为顶点的函数值-1,最大值在x=-1,x=3处取得,即为3,那么函数的值域为 ,选B.
,选B.点评:解决的关键是根据二次函数的性质求解值域,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
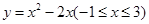 的值域是( )
的值域是( ) A.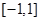 | B. | C.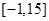 | D.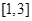 |
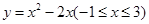 ,开口向上,对称轴x=1,那么在
,开口向上,对称轴x=1,那么在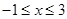 ,函数先递减在递增,可知函数的最小值为顶点的函数值-1,最大值在x=-1,x=3处取得,即为3,那么函数的值域为
,函数先递减在递增,可知函数的最小值为顶点的函数值-1,最大值在x=-1,x=3处取得,即为3,那么函数的值域为 ,选B.
,选B.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案