题目内容
11.计算:$\frac{{sin{{65}^o}+sin{{15}^o}sin{{10}^o}}}{{sin{{25}^o}-cos{{15}^o}cos{{80}^o}}}$.分析 由条件利用两角和差的三角公式、诱导公式化简所给的式子,可得结果.
解答 解:$\frac{{sin{{65}^o}+sin{{15}^o}sin{{10}^o}}}{{sin{{25}^o}-cos{{15}^o}cos{{80}^o}}}$=$\frac{sin(80°-15°)+sin15°sin10°}{sin(15°+10°)-cos15°cos80°}$=$\frac{sin80°cos15°}{sin15°cos10°}$=$\frac{cos15°}{sin15°}$=$\frac{cos(45°-30°)}{sin(45°-30°)}$
=$\frac{cos45°cos30°+sin45°sin30°}{sin45°co30°-cos45°sin30°}$=$\frac{\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{1}{2}}{\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}×\frac{1}{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{\sqrt{6}-\sqrt{2}}$=2+$\sqrt{3}$.
点评 本题主要考查两角和差的三角公式、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
19.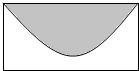 如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )
如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )
 如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )
如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则可以估计出阴影部分的面积约为( )| A. | $\frac{23}{11}$ | B. | $\frac{23}{10}$ | C. | $\frac{23}{6}$ | D. | $\frac{23}{5}$ |
6.使|x-4|+|x-5|<a有实数解的a为( )
| A. | a>1 | B. | 1<a<9 | C. | a>1 | D. | a≥1 |
3.下列函数中既是偶函数,又在区间(0,+∞)上单调递增的函数式( )
| A. | y=x3 | B. | y=-x3+1 | C. | y=|x|+1 | D. | y=2x |
1.不等式x2-5x-6>0的解集是( )
| A. | (-6,1) | B. | (-1,6) | C. | (-∞,-1)∪(6,+∞) | D. | (-∞,-6)∪(1,+∞) |
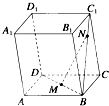 如图,已知ABCD-A1B1C1D1是平行六面体.设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的$\frac{3}{4}$分点,设$\overrightarrow{MN}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$+γ$\overrightarrow{AA1}$,试求α、β、γ的值.
如图,已知ABCD-A1B1C1D1是平行六面体.设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的$\frac{3}{4}$分点,设$\overrightarrow{MN}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$+γ$\overrightarrow{AA1}$,试求α、β、γ的值.