题目内容

18．已知正方形ABCD的边长为1，E、F分别为BC、CD的中点，沿线AF、AE、EF折起来，则所围成的三棱锥的体积为$\frac{1}{24}$．

分析 由题意图形折叠为三棱锥，直接求出三棱柱的体积即可．

解答 解：由题意图形折叠为三棱锥，底面为直角△EFC，AC⊥平面EFC，高为1，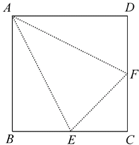
所以三棱柱的体积：$\frac{1}{3}$×$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{24}$，
故答案为：$\frac{1}{24}$．

点评 本题是基础题，考查几何体的体积的求法，注意折叠问题的处理方法，考查计算能力．

练习册系列答案
相关题目
8．已知数列{an}满足：a3=5，an+1=2an-1（n∈N*），则a1=2．
9．已知函数f（x）在R上满足f（x）=2f（2-x）+ex-1+x2，则曲线y=f（x）在点（1，f（1））处的切线方程是x-y-3=0．
6．已知$\overrightarrow a=\overrightarrow{e_1}-\overrightarrow{e_2}$，$\overrightarrow b=4\overrightarrow{e_1}+3\overrightarrow{e_2}$，其中$\overrightarrow{e_1}$=（1，0），$\overrightarrow{e_2}$=（0，1），计算$\overrightarrow a$•$\overrightarrow b$，|$\overrightarrow a$+$\overrightarrow b$|的值．
13．现有4个同学去看电影，他们坐在了同一排，且一排有6个座位．问
（1）所有可能的坐法有多少种？
（2）此4人中甲、乙两人相邻的坐法有多少种？（结果均用数字作答）
3．若二次函数f（x）=x2-2x+2在区间[t，t+1]上的最小值为g（t），求函数g（t）在t∈[-3，-2]时的最值．
10．若a，b∈R，则不等式|2+ax|≥|2x+b|的解集为R的充要条件是（　　）
A．a=±2B．a=b=±2C．ab=4且|a|≤2D．ab=4且|a|≥2
7．已知数列{an}是公差不为零的等差数列，a1=1，且a1、a3、a13是等比数列．
（1）求数列{an}的通项公式；
（2）求数列{2${\;}^{{a}_{n}}$}的前n项和Sn ．
11．计算：$\frac{{sin{{65}^o}+sin{{15}^o}sin{{10}^o}}}{{sin{{25}^o}-cos{{15}^o}cos{{80}^o}}}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网