题目内容
【题目】已知f(xy)=f(x)+f(y).
(1) 若x,y∈R,求f(1),f(-1)的值; (2)若x,y∈R,判断y=f(x)的奇偶性;
(3)若函数f(x)在其定义域(0,+∞)上是增函数,f(2)=1,f(x)+f(x-2)≤3,求x的取值范围。
【答案】(1)f(1)=0.f(-1)=0(2)偶函数(3) (2,4]
【解析】
(1)利用赋值法可得f(1),f(-1)的值;(2)令y=-1 ,则可得f(-x)=f(x),即得结果,(3)先根据定义得f[x(x-2)]≤f(8),再根据单调性化简不等式,解得结果.
解:(1)令x=y=1,则f(1)=f(1)+f(1),所以f(1)=0.
又令x=y=-1,则f(1)=f(-1)+f(-1), 所以f(-1)=0.
(2)令y=-1,则f(-x)=f(x)+f(-1),由(1)知f(-1)=0,
所以f(-x)=f(x),即函数f(x)为偶函数.
(3)因为f(4)=f(2)+f(2)=1+1=2,所以f(8)=f(2)+f(4)=1+2=3,
因为f(x)+f(x-2)≤3, 所以f[x(x-2)]≤f(8),
因为f(x)在(0,+∞)上是增函数,所以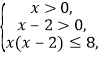 即
即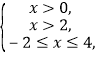
所以x的取值范围是(2,4].

【题目】“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手大多在以下两个年龄段:21~30,31~40(单位:岁),统计这两个年龄段选手答对歌曲名称与否的人数如图所示.
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(1)写出2×2列联表,并判断是否有90%的把握认为答对歌曲名称与否和年龄有关,说明你的理由.(下面的临界值表供参考)
P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)在统计过的参考选手中按年龄段分层选取9名选手,并抽取3名幸运选手,求3名幸运选手中在21~30岁年龄段的人数的分布列和数学期望.

