Question

【题目】已知函数，其中且．

（Ⅰ）当时，求函数的值域；

（Ⅱ）当在区间上为增函数时，求实数的取值范围.

Answer 1

【答案】(1) ;(2) .

【解析】试题分析：（Ⅰ）把a＝代入函数解析式，可得定义域为R，利用配方法求出真数的范围，结合复合函数单调性求得函数f（x）的值域；
（Ⅱ）对a＞1和0＜a＜1分类讨论，由ax2-x+1在上得单调性及ax2-x+1＞0对x∈恒成立列不等式组求解a的取值范围，最后取并集得答案．

试题解析：

（Ⅰ）当时，真数恒成立，

故定义域为，

又∵真数，且函数在单调递减

∴，即函数的值域为.

（Ⅱ）依题意可知，

i）当时，由复合函数的单调性可知，必须在上递增，且对恒成立,

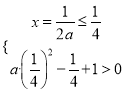故有解得： .

ii）当时，由同理必须在上递减，且对恒成立

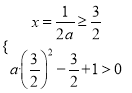故有解得：

综上，实数的取值范围为.