题目内容
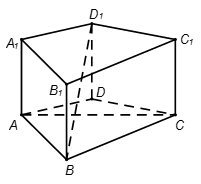
如图,在直三棱柱(即侧棱与底面垂直的三棱柱)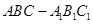 中,
中,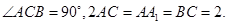
(I)若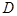 为
为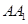 的中点,求证:平面
的中点,求证:平面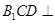 平面
平面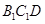 ;
;
(II)若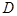 为线段
为线段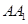 上一点,且二面角
上一点,且二面角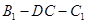 的大小为
的大小为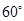 ,试确定
,试确定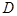 的位置.
的位置.
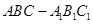 中,
中,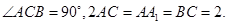

(I)若
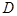 为
为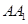 的中点,求证:平面
的中点,求证:平面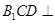 平面
平面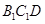 ;
;(II)若
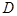 为线段
为线段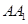 上一点,且二面角
上一点,且二面角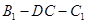 的大小为
的大小为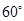 ,试确定
,试确定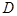 的位置.
的位置.(I)略;(II)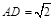 .
.
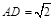 .
.试题分析:(I)可以转为证线面垂直或利用空间向量证明面面垂直;(II)可利用
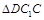 的面积求
的面积求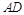 也可利用空间向量求
也可利用空间向量求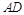 .
.试题解析:方法一:(I)证明:∵
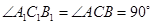 ,∴
,∴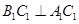 .
. 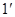
又由直三棱柱的性质知
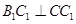 ,
, 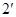
∴
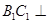 平面
平面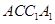 ,∴
,∴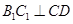 , ①
, ①
由
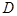 为
为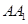 的中点,可知
的中点,可知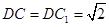 ,
,∴
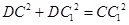 ,即
,即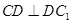 , ②
, ②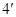
又
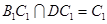 ③
③由①②③可知
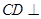 平面
平面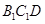 ,
, 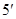
又
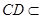 平面
平面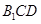 ,故平面
,故平面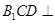 平面
平面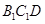 .
. 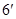
(II)解:由(I)可知
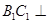 平面
平面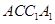 ,在平面
,在平面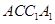 内过
内过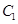 作
作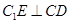 ,交
,交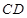 或其延长线于
或其延长线于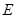 ,连接
,连接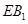 ,∴
,∴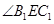 为二面角
为二面角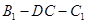 的平面角,
的平面角, 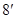
∴
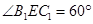 .由
.由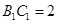 知,
知,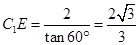 ,设
,设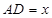 ,则
,则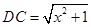 .
.∵
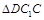 的面积为
的面积为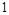 ,∴
,∴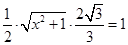 .
. 
解得
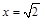 ,即
,即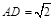 .
. 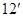
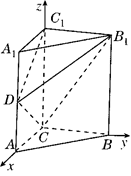
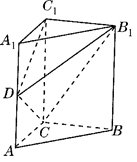
方法二:(I)证明:如图,以
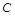 为坐标原点,
为坐标原点,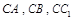 所在的直线分别为
所在的直线分别为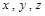 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则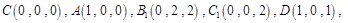 即
即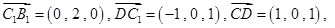
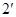
由
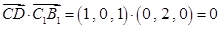 ,得
,得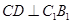 ;
; 
同理可证
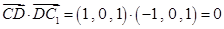 ,得
,得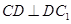 .
. 
又
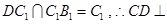 平面
平面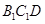 .
. 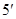
又
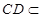 平面
平面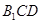 ,∴平面
,∴平面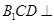 平面
平面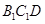 .
. 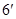
(II)解:设
 ,则
,则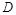 点坐标为
点坐标为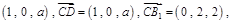
设平面
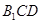 的一个法向量为
的一个法向量为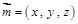 .
.则
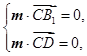
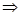
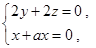 令
令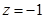 .
.得
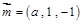 ,
, 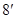
又平面
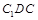 的一个法向量为
的一个法向量为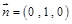 ,
, 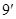
则由
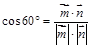 ,得
,得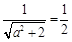 ,
, 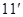
即
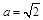 ,故
,故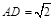 . ……
. ……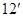

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 ,
, ,
, ,
,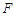 为线段
为线段 的中点.
的中点.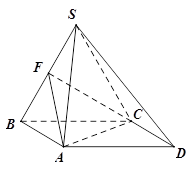
 平面
平面 ;
; 与面
与面 所成二面角大小.
所成二面角大小. 均为全等的直角梯形,且
均为全等的直角梯形,且 ,
, .
.
 平面
平面 ;
; 的余弦值.
的余弦值. 中,
中, 平面
平面 .
.
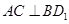 的充分条件,并给予证明;
的充分条件,并给予证明;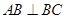 ,②
,②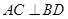 ;③
;③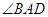 为锐角,求平面
为锐角,求平面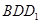 与平面
与平面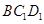 所成锐二面角
所成锐二面角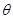 的取值范围.
的取值范围. 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: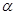 与平面
与平面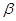 相交于直线
相交于直线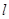 ,直线
,直线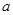 在平面
在平面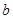 在平面
在平面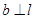 ,则“
,则“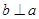 ”是“
”是“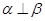 ”的( )
”的( ) ,
, 为直线,
为直线, 为平面,若
为平面,若 ∥
∥ ,则
,则 若
若 ,则
,则 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( ) 或
或 
 或
或 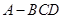 中,
中,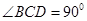 ,
, 平面
平面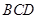 ,
,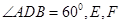 分别是直线
分别是直线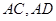 上的点,且
上的点,且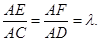
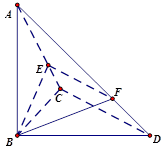
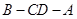 平面角的余弦值
平面角的余弦值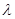 为何值时,平面
为何值时,平面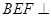 平面
平面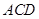
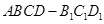 中,四边形
中,四边形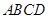 为菱形,
为菱形,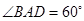 ,
,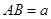 ,面
,面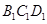 ∥面
∥面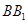 、
、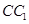 、
、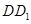 都垂直于面
都垂直于面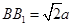 ,
,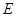 为
为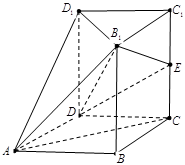
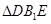 为等腰直角三角形;
为等腰直角三角形;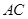 ∥面
∥面 .
.