题目内容
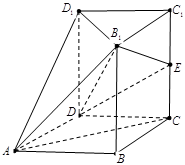
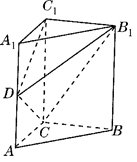
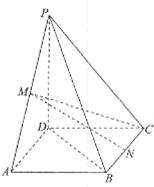
如图,几何体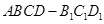 中,四边形
中,四边形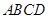 为菱形,
为菱形,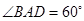 ,
,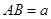 ,面
,面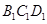 ∥面
∥面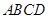 ,
,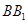 、
、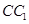 、
、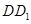 都垂直于面
都垂直于面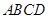 ,且
,且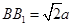 ,
,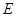 为
为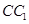 的中点.
的中点.
(Ⅰ)求证: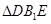 为等腰直角三角形;
为等腰直角三角形;
(Ⅱ)求证: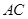 ∥面
∥面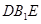 .
.
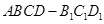 中,四边形
中,四边形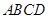 为菱形,
为菱形,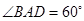 ,
,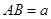 ,面
,面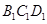 ∥面
∥面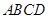 ,
,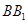 、
、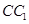 、
、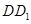 都垂直于面
都垂直于面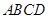 ,且
,且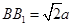 ,
,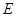 为
为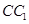 的中点.
的中点.
(Ⅰ)求证:
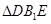 为等腰直角三角形;
为等腰直角三角形;(Ⅱ)求证:
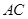 ∥面
∥面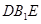 .
.(1)根据边长和勾股定理来证明即可
(2)要证明线面平行,则要结合判定定理来加以证明即可。
(2)要证明线面平行,则要结合判定定理来加以证明即可。
试题分析:解:(I)连接
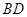 ,交
,交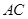 于
于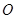 ,因为四边形
,因为四边形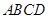 为菱形,
为菱形,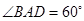 ,所以
,所以
因为
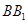 、
、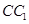 都垂直于面
都垂直于面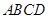 ,
,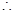
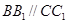 又面
又面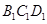 ∥面
∥面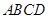 ,
,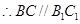
所以四边形
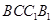 为平行四边形 ,则
为平行四边形 ,则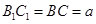 2分
2分因为
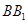 、
、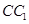 、
、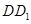 都垂直于面
都垂直于面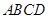 ,则
,则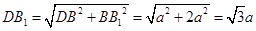

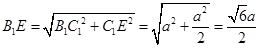 4分
4分所以
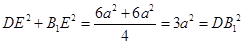 所以
所以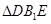 为等腰直角三角形 6分
为等腰直角三角形 6分(II)取
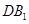 的中点
的中点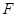 ,连接
,连接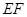 、
、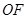 (略)
(略)点评:主要是考查了线面平行以及线线垂直的证明,属于中档题。

练习册系列答案
相关题目
 中,
中,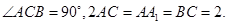
 为
为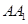 的中点,求证:平面
的中点,求证:平面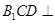 平面
平面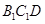 ;
;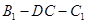 的大小为
的大小为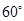 ,试确定
,试确定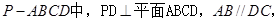
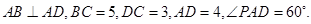
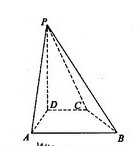
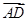 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥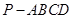 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);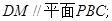
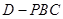 的体积.
的体积.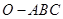 的侧棱
的侧棱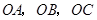 两两垂直,且
两两垂直,且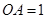 ,
,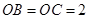 ,
,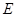 是
是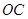 的中点.
的中点.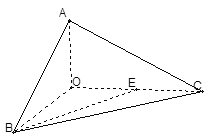
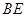 与
与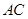 所成的角的余弦值
所成的角的余弦值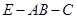 的余弦值
的余弦值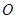 点到面
点到面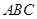 的距离
的距离
 的棱长为1,
的棱长为1, 分别为线段
分别为线段 上的动点,则三棱锥
上的动点,则三棱锥 的体积为________.
的体积为________.
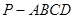 中,底面
中,底面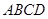 是正方形,
是正方形, 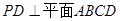 ,
,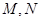 分别为
分别为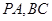 的中点,且
的中点,且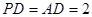 .
.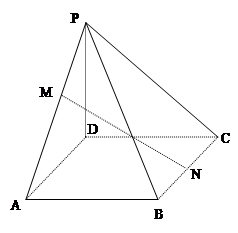
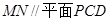 ;
;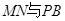 所成的角的余弦值
所成的角的余弦值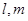 是不同的两条直线,
是不同的两条直线,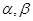 是不重合的两个平面,则下列命题中为真命题的是( )
是不重合的两个平面,则下列命题中为真命题的是( )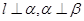 ,则
,则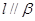
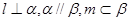 ,则
,则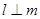
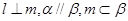 ,则
,则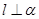
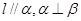 ,则
,则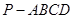 中,底面
中,底面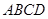 是矩形,
是矩形,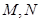 分别为
分别为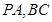 的中点,
的中点,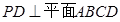 ,且
,且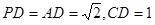
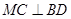 ;
;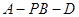 的余弦值。
的余弦值。