题目内容
在如图所示的几何体中,四边形 均为全等的直角梯形,且
均为全等的直角梯形,且 ,
, .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
 均为全等的直角梯形,且
均为全等的直角梯形,且 ,
, .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.(Ⅰ)证明过程详见解析;(Ⅱ)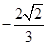 .
.
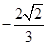 .
.试题分析:本题考查线面平行的判定以及二面角的求法.线面平行的判断:①判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;②性质:如果两个平面平行,其中一个平面内的直线必平行于另一个平面;③性质:如果两条平行线中的一条平行于一个平面,那么另一条也平行于这个平面或在这个平面内;④性质:如果一条直线平行于两个平行平面中的一个,那么这条直线也平行于另一个平面或在这个平面内;⑤性质:如果一个平面和平面外的一条直线都垂直于同一平面,那么这条直线和这个平面平行.第一问是利用线面平行的判定定理证明;第二问建立空间直角坐标系是关键,利用向量法得到平面
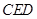 的一个法向量为
的一个法向量为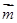 ,和平面
,和平面 的一个法向量为
的一个法向量为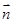 ,再利用夹角公式求夹角的余弦,但是需判断夹角是锐角还是钝角,进一步判断余弦值的正负.
,再利用夹角公式求夹角的余弦,但是需判断夹角是锐角还是钝角,进一步判断余弦值的正负.试题解析:(Ⅰ)连结
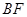 ,由题意,可知
,由题意,可知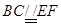 ,
,故四边形
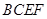 是平行四边形,所以
是平行四边形,所以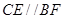 .
.又
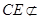 平面
平面 ,
,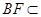 平面
平面 ,
,所以
 平面
平面 . 5分
. 5分
(Ⅱ)由题意,
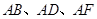 两两垂直,
两两垂直,以
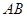 为
为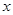 轴,
轴,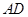 为
为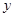 轴建立空间直角坐标系
轴建立空间直角坐标系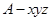 .
.设
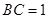 ,则
,则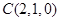 ,
,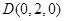 ,
,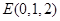 ,
,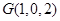 .
.设平面
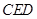 的一个法向量为
的一个法向量为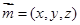 ,
,则
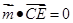 ,
,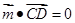 ,
,又
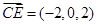 ,
,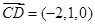 ,
,所以
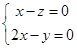 ,取
,取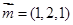 .
.同理,得平面
 的一个法向量为
的一个法向量为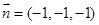 .
.因为
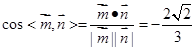 ,又二面角
,又二面角 为钝角,
为钝角,所以二面角
 的余弦值
的余弦值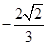 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,底面
中,底面 为菱形,其中
为菱形,其中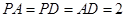 ,
, ,
, 为
为 的中点.
的中点.
 ;
; 平面
平面 为
为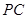 的中点,求四棱锥
的中点,求四棱锥 的体积.
的体积.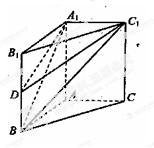
 的边长为4,
的边长为4, ,
, .将菱形
.将菱形 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
 平面
平面 ;
;
 平面
平面 ;
; 的余弦值.
的余弦值. 中,
中,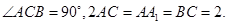
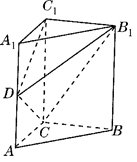
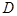 为
为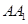 的中点,求证:平面
的中点,求证:平面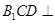 平面
平面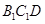 ;
;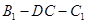 的大小为
的大小为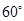 ,试确定
,试确定 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是 ( )
是一个平面,则下列命题正确的是 ( ) ,
,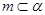 ,则
,则
 ,则
,则
 ,
, ,则
,则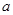 的等边三角形
的等边三角形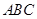 的中线
的中线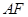 与中位线
与中位线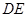 交于点
交于点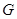 ,已知
,已知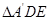 (
(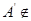 平面
平面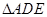 绕
绕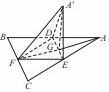
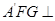 平面
平面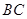 //平面
//平面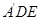 ;
;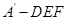 的体积最大值为
的体积最大值为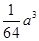 ;
;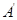 在平面
在平面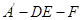 大小的范围是
大小的范围是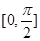 .
.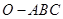 的侧棱
的侧棱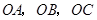 两两垂直,且
两两垂直,且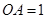 ,
,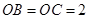 ,
,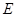 是
是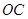 的中点.
的中点.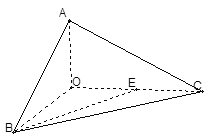
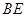 与
与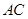 所成的角的余弦值
所成的角的余弦值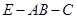 的余弦值
的余弦值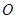 点到面
点到面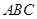 的距离
的距离