题目内容

9．已知数列{an}中，a1=a2=1，且an+2-an=1，则数列{an}的前100项和为（　　）
A．2550B．2600C．2651D．2652

分析 a1=a2=1，且an+2-an=1，可得数列{an}奇数项与偶数项分别成等差数列，公差与首项都为1．利用等差数列的前n项和公式即可得出．

解答 解：∵a1=a2=1，且an+2-an=1，
∴数列{an}奇数项与偶数项分别成等差数列，公差与首项都为1．
∴数列{an}的前100项和=（a1+a3+…+a99）+（a2+a4+…+a100）
=$[50×1+\frac{50×49}{2}×1]×2$
=2550．
故选：A．

点评 本题考查了等差数列的定义通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
4．已知定义域为（1，+∞）的函数f（x）满足：
①对任意x∈（1，+∞），恒有f（2x）=f（x）+1成立；
②当满足x∈（1，2]时，f（x）=sin$\frac{πx}{2}$．求：
（1）f（4）；
（2）f（2n）（n∈N*）．
5．若方程log2x+2x-a=0在区间[1，2]内有解，则实数a的取值范围是（　　）
A．[2，3]B．[2，4]C．[2，5]D．[2，6]
17．已知f（x）=$\left\{{\begin{array}{l}{{x^2}+1，x≥0}\\{-2x，x＜0}\end{array}}$，
（1）求f（0）和f[f（0）]的值；
（2）若f（x0）=10，求出x0所有可能取的值．
4．已知集合A=$\{a|\frac{x+a}{{{x^2}-1}}=1有唯一实数解\}$，则集合A={-$\frac{5}{4}$，-1，1}．
14．已知tan（$\frac{π}{4}$+α）=$\frac{1}{7}$，α∈（$\frac{π}{2}$，π），则tanα的值是-$\frac{3}{4}$；sin2α+sinαcosα的值是$-\frac{3}{25}$； $cos（{α-\frac{π}{6}}）$的值是$\frac{{3-4\sqrt{3}}}{10}$．
1．计算lg$\frac{5}{2}$+2lg2-（$\frac{1}{2}$）-1=（　　）
A．2B．1C．0D．-1
18．已知映射f：x→lgx+1，则像2在f作用下的原像为（　　）
A．lg2+1B．1C．10D．100
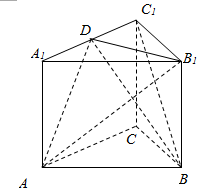19．如图，正三棱柱ABC-A1B1C1中，底面边长为2，侧楞长为$\sqrt{2}$，D为A1C1中点．
（1）求证：BC1∥平面AB1D；
（2）求证：平面AB1D⊥平面AA1C1C；
（3）求点B到平面AB1D的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网