题目内容
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
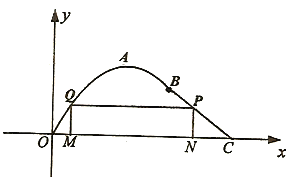
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
【答案】(1) 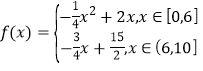 .
.
(2)当OM长为1千米时,绿化带的总长度最长![]() .
.
【解析】试题分析:(1)曲线段![]() 过点
过点![]() ,且最高点为
,且最高点为![]() ,可列出方程组,求解
,可列出方程组,求解![]() 的值,可得当
的值,可得当![]() 上函数的解析式,后一部分为线段
上函数的解析式,后一部分为线段![]() ,
,![]() ,可得
,可得![]() 上的解析式;(2)求出绿化带的总长度,可得二次函数即可得出结论.
上的解析式;(2)求出绿化带的总长度,可得二次函数即可得出结论.
试题解析:(1)因为曲线段OAB过点O,且最高点为![]()
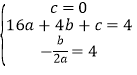 ,解得
,解得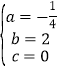 (也可以设成顶点式)
(也可以设成顶点式)
所以,当![]() 时,
时,![]()
因为后一部分为线段BC,![]() ,当
,当![]() 时,
时,![]() ……6分
……6分
综上,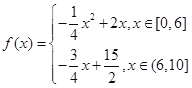
(2)设![]() ,则
,则![]()
由![]() , 得
, 得![]() ,
,
所以点![]()
所以,绿化带的总长度![]()
![]() ……13分
……13分
当![]() 时,
时,![]()
所以,当OM长为1千米时,绿化带的总长度最长

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】某学习小组在暑期社会实践活动中,通过对某商店一种商品销售情况的调查发现:该商品在过去的一个月内(以30天计)的日销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() 为正常数).该商品的日销售量
为正常数).该商品的日销售量![]() (个)与时间
(个)与时间![]() (天)部分数据如下表所示:
(天)部分数据如下表所示:
| 10 | 20 | 25 | 30 |
| 110 | 120 | 125 | 120 |
已知第10天该商品的日销售收入为121元.
(I)求![]() 的值;
的值;
(II)给出以下二种函数模型:
①![]() ,②
,②![]() ,
,
请你根据上表中的数据,从中选择你认为最合适的一种函数来描述该商品的日销售量![]() 与时间
与时间![]() 的关系,并求出该函数的解析式;
的关系,并求出该函数的解析式;
(III)求该商品的日销售收入![]() (元)的最小值.
(元)的最小值.
(函数![]() ,在区间
,在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.性质直接应用.)
上单调递增.性质直接应用.)
