Question

【题目】已知函数（0＜φ＜π）

（1）当φ时，在给定的坐标系内，用“五点法”做出函数f（x）在一个周期内的图象；

（2）若函数f（x）为偶函数，求φ的值；

（3）在（2）的条件下，求函数在[﹣π，π]上的单调递减区间．

Answer 1

【答案】（1）见解析；（2）φ；（3）[0，π]

【解析】

（1）先列表描点即可画出图像；（2）由偶函数求解即可；（3）求f（x）＝的单调减区间则可求

（1）当φ时，，

列表如下：

	0
x
	0	2	0	﹣2	0

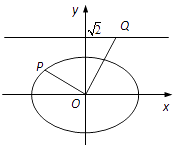
用“五点法”作出函数的一个周期内的图象，如图所示；

（2）∵函数f（x）为偶函数，∴，

∵0＜φ＜π，∴φ；

（3）由（2）得，f（x）＝ ，

当x∈[﹣π，π]时，∴，

∴当，即x∈[0，π]时f（x）单调递减．

∴函数在[﹣π，π]上的单调递减区间[0，π]．